论文阅读Learning Imbalanced Datasets with Label-Distribution-Aware Margin Loss

Learning Imbalanced Datasets with Label-Distribution-Aware Margin Loss

论文：链接: link

NIPS 2019

Abstract

当训练数据集存在严重的类不平衡时，深度学习算法的表现可能会很差，但测试标准需要对不太频繁的类进行良好的泛化。
我们设计了两种新的方法来提高这种情况下的性能。首先，我们提出了一个理论上的标签分布感知边际损失(LDAM)，其动机是最小化基于边际的泛化边界。在训练过程中，这种损失取代了标准的交叉熵目标，并可以应用于先前的训练策略，如重加权或重采样类不平衡。其次，我们提出了一个简单而有效的训练计划，将重新加权推迟到初始阶段之后，允许模型学习初始表示，同时避免了与重新加权或重新抽样相关的一些复杂性。我们在几个基准视觉任务上测试了我们的方法，包括真实世界的不平衡数据集iNaturalist 2018。我们的实验表明，这两种方法中的任何一种都可以比现有的技术有所改进，它们的结合甚至可以获得更好的性能增益。

Introduction

现代真实大尺度数据集往往具有长尾标签分布[V an Horn and Perona, 2017, Krishna et al.， 2017, Lin et al.， 2014, Everingham et al.， 2010, Guo et al.， 2016, Thomee et al.， 2015, Liu et al.， 2019]。在这些数据集中，深度神经网络在较少代表的类上表现较差[He和Garcia, 2008, V an Horn和Perona, 2017, Buda等人，2018]。如果考试标准更多地强调少数类别，这尤其有害。例如，均匀标签分布的精度或所有类中的最小精度都是这种标准的例子。这是许多应用中常见的场景[Cao等人，2018,Merler等人，2019,Hinnefeld等人，2018]，由于各种实际问题，如可转移到新领域，公平性等。学习的两种常见的方法长尾例子和重采样的数据权重损失SGD mini-batch中的示例(见[布达et al ., 2018年,黄et al ., 2016年,崔et al ., 2019年,他和加西亚,2008年,他和马,2013年,乔et al ., 2002)和引用其中)。他们都设计了一种预期更接近测试分布的训练损失，因此可以在频繁类和少数类的准确性之间实现更好的权衡。然而，由于我们对少数类的基本信息较少，而且所部署的模型往往庞大，因此对少数类的过度拟合似乎是改进这些方法的挑战之一。

我们建议将少数类的正则化程度比频繁类的正则化程度更高，从而在不牺牲模型拟合频繁类的能力的前提下，提高少数类的泛化误差。实现这个概念需要一个数据依赖或标签依赖的正则化器——与标准的2正则化不同，它不仅依赖于权重矩阵，还依赖于标签——来区分频繁类和少数类。对依赖数据的正则化器的理论理解是稀疏的(参见Wei和Ma, 2019, Nagarajan和Kolter, 2019, Arora等人，2018)。

我们将探索一个最简单和最容易理解的数据相关属性:训练示例的边界。鼓励较大的边际可以被视为正则化，作为标准的泛化误差边界(例如，[Bartlett等人，2017,Wei等人，2018])，依赖于所有例子中最小边际的倒数。受关于少数类的泛化问题的激励，我们转而研究每个类的最小边际，并得到每个类和统一标签的测试误差边界。2最小化所得到的边界可以在类的边界之间找到最优的平衡。图1给出了二进制分类的示例。

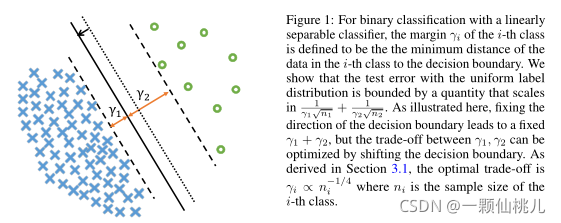
图1:对于线性可分分类器的二值分类，定义第i类的边缘γi为第i类数据到决策边界的最小距离。我们证明了均匀标签分布下的检验误差是由一个尺度为1 γ1√n1+ 1 γ2√n2的量所限制的。如这里所示，确定决策边界的方向将导致固定的γ1+ γ2，但是可以通过改变决策边界来优化γ1、γ2之间的权衡。如3.1节所推导的，最佳权衡是γi∝n−1/4 i，其中niis第i类的样本量。

受到这个理论的启发，我们设计了一个标签分布感知的损失函数，鼓励模型在每个类别的边际之间有最优的权衡。通过鼓励少数群体获得更大的利润，拟议损失扩大了现有的软利润损失[Wang et al.， 2018a]。作为一种依赖于标签的正则化技术，我们的修正损失函数与重加权重采样方法正交。事实上，我们还设计了一个延迟的重新平衡优化过程，允许我们以更有效的方式将重新加权策略与我们的损失(或其他损失)结合起来。

总之，我们的主要贡献是:(1)我们设计了一个感知标签分布的损失函数，以鼓励少数类获得更大的利润;(2)我们提出了一个简单的延迟重平衡优化程序，以更有效地应用重加权;(iii)我们的实际实现显示了几个基准视觉任务的显著改进，如人工不平衡CIFAR和Tiny ImageNet [tin]，以及真实世界的大规模不平衡数据集iNaturalist ’ 18 [V an Horn et al.， 2018]。

2.Related Works

现有的不平衡数据集学习算法可分为两类:重采样算法和重加权算法。

重采样。有两种类型的重采样技术:over-sampling少数类和under-sampling频繁的类。不足采样的缺点是它丢弃了大量的数据，因此在数据极不平衡的情况下是不可行的。在很多情况下，过采样是有效的，但会导致少数类的过拟合。对于少数群体，更强的数据增强有助于缓解过拟合。

权重。成本敏感重加权为不同类别甚至不同样本分配(自适应)权重。普通方案按其频率的倒数对类别进行权重调整[Huang等人，2016,2019,Wang等人，2017]。在极端的数据不平衡设置和大规模场景下，重加权方法往往会使深度模型的优化变得困难[Huang等，2016,2019]。Cui等人[2019]观察到通过逆类频率重新加权在频繁类上的性能较差，因此提出通过逆有效样本数重新加权。这是我们根据经验进行比较的主要前期工作。

另一条工作线根据每个样本的属性为它们分配权重。Focal loss [Lin et al.， 2017]对分类良好的例子进行了降权重;Li et al.[2018]建议一种改进的技术，该技术对具有非常小梯度或大梯度的示例进行降权重，因为具有小梯度的示例分类良好，而具有大梯度的示例往往是离群值。

在最近的一项研究中[Byrd和Lipton, 2019]， Byrd和Lipton研究了重要性权重的影响，表明在不采用正则化的情况下，经验上的重要性权重没有显著的影响，这与[Soudry等人，2019]的理论预测一致。2018]，无需正则化的逻辑回归收敛于最大裕度解。在我们的工作中，我们明确地鼓励稀有类有更高的边际，因此我们不会收敛到最大边际的解决方案。此外，在我们的实验中，我们采用非平凡的2正则化来获得最佳的泛化性能。我们还发现，延迟重加权(或延迟重采样)比训练开始时的重新加权和重采样更有效。

与上述论文相反，我们的主要技术旨在通过应用正交于重加权方案的额外正则化来改进少数类的推广。我们还提出了一个延迟重平衡优化程序，以改进一般重权方案的优化和泛化。

利润损失。铰链损耗常被用于获得“max-margin”分类器，尤其是在支持向量机中[Suykens和V anddewalle, 1999]。最近，Large-Margin Softmax [Liu et al.， 2016]、Angular Softmax [Liu et al.， 2017a]和Additive Margin Softmax [Wang et al.， 2018a]被提出，通过引入角边界的思想来最小化预测中的类内变化，并扩大类间边界。与这些论文中阶级独立的边际不同，我们的方法鼓励为少数阶级提供更大的边际。[Li et al.， 2002]和最近的研究[Khan et al.， 2019, Li et al.， 2019]也提出并研究了不平衡数据集的不均匀边缘。我们的理论将这个想法置于一个更理论化的基础上，通过提供一个具体的公式，期望的阶级边际和良好的经验进步。

领域适应中的标签转移。学习不平衡的数据集问题也可以看作迁移学习或领域适应中的标签转移问题(对此我们参考了调查[Wang and Deng, 2018]及其参考文献)。在典型的标签位移公式中，难点是检测和估计标签位移，估计标签位移后再进行重加权或重采样。
我们正在解决一个很大不同的问题:当标签移位已知时，我们是否能做得比重新加权或重新抽样更好?事实上，我们的算法可以用来替代最近一些有趣的检测和纠正标签偏移的重新加权步骤。

分布鲁棒优化(DRO)是领域自适应的另一种技术(参见[Duchi等人，Hashimoto等人，2018,Carmon等人，2019]及其参考文献)。然而，该公式假设不知道目标标签的分布超过了偏移量的界限，这使得问题非常具有挑战性。
在这里，我们假设测试标签分布的知识，利用它，我们设计了有效的方法，可以轻松地扩展到大规模的视觉数据集，有显著的改进。

元学习。元学习还被用于改善不平衡数据集或少数镜头学习设置的性能。我们建议读者参考[Wang et al.， 2017, Shu et al.， 2019, Wang et al.， 2018b]及其参考文献。到目前为止，我们通常认为，我们的方法修正损失的计算效率高于基于元学习的方法。

3 Main Approach

3.1 Theoretical Motivations理论动机

问题设置和符号。 我们假设输入空间是Rd和标签空间是{1，…k}。设x表示输入，y表示对应的标签。我们假设在训练和测试时，类条件分布P(x | y)是相同的。设Pj表示类条件分布，即Pj= P(x | y = j)，我们用Pbalto表示均衡检验分布，即先对一类均匀抽样，然后从Pj中抽样数据。

对于输出k logits的模型f: Rd→rk，我们使用Lbal[f]表示均衡数据分布的标准0-1检验误差:

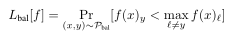
类似地，类j的误差Lj被定义为：

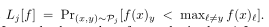
假设我们有一个训练数据集{(xi, yi)}ⁿ i=1。设nj是类j中的样本数，Sj= {i: yi= j}表示类j对应的样本索引，定义一个样本(x, y)的边界为

将j类的培训裕度定义为:

我们考虑可分离的情况(意思是所有的训练例子都是正确分类的)，因为神经网络通常是过度参数化的，可以很好地拟合训练数据。我们还注意到所有类的最小边际，γmin= min{γ1，…， γk}，是过去研究的训练边际的经典概念[Koltchinskii等人，2002]。

细粒度泛化误差边界。设F是假设类的族。设C(F)是假设类F的适当复杂度度量。 .最近有大量的神经网络的复杂性的度量工作,下面我们讨论正交于精确的选择。
当训练分布和测试分布相同时，典型的泛化误差边界尺度为C(F)/√n。也就是说，在我们的例子中，如果测试分布和训练分布一样不平衡，那么

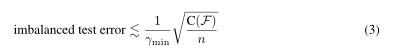
注意，边界与标签分布无关，只涉及所有示例的最小边距和数据点的总数。通过考虑每个类的边界，我们将这种界限扩展到具有平衡测试分布的集合。正如我们将看到的，下面更细粒度的界限允许我们设计新的训练损失函数，该函数是针对不平衡数据集定制的。

定理1(定理2的非正式简化版)。当训练数据的随机性有高概率(1−n⁻⁵)时，类j的误差Lj为

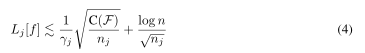
我们使用的地方。隐藏常数因子。直接的结果是，

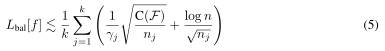
Class-distribution-aware保证金交易。每个类的泛化误差界(4)表明，如果我们希望改进少数类(那些具有小nj的类)的泛化，我们应该致力于为它们强制更大的边际γj。然而，对少数族裔实行更大的边际政策可能会损害普通阶层的边际。阶级边缘之间的最佳取舍是什么?一般情况下的答案可能是困难的，但幸运的是，我们可以得到二元分类问题的最优权衡。

当k = 2个类时，我们的目标是优化(5)中提供的平衡泛化误差界，它可以简化为(通过去除低阶项log n/√nj和公因式C(F))

乍一看，由于γ1和γ2是权矩阵的复杂函数，因此很难理解最优边界。然而，我们可以计算出γ1和γ2之间的相对尺度。假设γ1， γ2> 0最小化上述方程，我们观察到任何γ0 1= γ1−δ和γ0 2= γ2+δ(对于δ∈(−γ2， γ1))都可以通过相同的权重矩阵实现，但偏移了偏差项(见图1的说明)。因此，对于γ1， γ2为最优，它们应满足

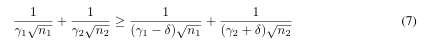
上面的方程暗示了这一点

请参阅a节中详细的推导。

速率与慢速率的对比，以及对边际选择的影响。定理1中的界限不一定很紧。以1/√n(或1/√nihere with unbalanced classes)为尺度的泛化边界通常被称为“慢速率”，以1/n为尺度的泛化边界被称为“快速率”。有了深度神经网络，当模型足够大的时候，这些边界有可能被提高到最快的速度。参见[魏和马，2019]了解近期的一些进展。在这些情况下，我们可以推导出边际的最佳取舍为ni∝n−1/3 i。

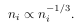
3.2 Label-Distribution-Aware Margin Loss

受3.1节中两个类的类边界之间的权衡的启发，我们建议对该形式的多个类强制类依赖边界

我们将设计一个软裕度损失函数，以鼓励网络具有上述裕度。设(x, y)是一个例子，f是一个模型。为简单起见，我们使用zj= f(x) j来表示第j个类的模型的第j个输出。最自然的选择将是铰链损失的多级扩展:

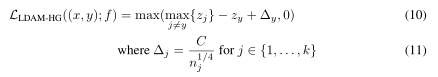
这里C是要调优的超参数。为了更容易地调整边界，我们按照之前的工作[Wang et al.， 2018a]，通过将最后一个隐藏激活归一化到“2norm 1”，并将最后一个全连接层的权向量归一化到“2norm 1”，有效地对logits(损失函数的输入)进行归一化。经验上，铰链损耗的不平滑性可能给优化带来困难。铰链损耗的平滑松弛为以下带有强制边界的交叉熵损耗:

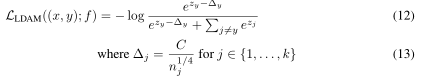
在之前的工作[Liu et al.， 2016, 2017a, Wang et al.， 2018a]中，训练集通常是平衡的，选取边际∆y为标签独立常数C，而我们的边际取决于标签分布。

备注:细心的读者可能会发现损失LLDAMsomewhat权重的因为在二进制分类情况下,模型输出一个实数是通过乙状结肠转化为一个概率,——这两种方法的梯度变化的一个例子一个标量的因素。然而，我们注意到两个关键的区别:重新加权引入的标量因子只依赖于类，而LLDAM引入的标量还依赖于模型的输出;对于多类分类问题，所提出的损失lldama以比仅引入标量因子更复杂的方式影响示例的梯度。此外，最近的研究表明，在可分离假设下，物流损失(弱正则化[Wei et al.， 2018]或未正则化[Soudry et al.， 2018])给出了最大裕度解，根据其定义，该解不受任何重加权的影响。这进一步表明，正如我们在实验中所看到的，损失lldamas和重加权可以相互补充。(重新加权会影响不可分离数据情况下的裕度，这将留给以后的工作。)

3.3 Deferred Re-balancing Optimization Schedule延迟重平衡优化计划

代价敏感的重加权和重抽样是处理不平衡数据集的两种知名且成功的策略，因为在预期中，它们有效地使不平衡的训练分布更接近均匀的测试分布。应用这些技术的已知问题是(a)当模型是深度神经网络时，对少数类中的例子重新抽样往往会导致少数类过度拟合(例如，[Cui et al.， 2019])，(b)对少数族裔班的损失进行加权会导致优化的困难和不稳定性，尤其是在班级极度不平衡的情况下[Cui et al.， 2019, Huang et al.， 2016]。事实上，Cui等人[2019]开发了一种新颖而复杂的学习率计划来应对优化困难。

我们根据经验观察，在按以下意义退火学习率之前，重新加权和重新抽样都不如香草经验风险最小化(ERM)算法(其中所有训练示例具有相同的权重)。再加权和重采样退火学习率之前产生的特征比ERM产生的特征差。(参见图6，通过在大型平衡数据集上的特征上训练线性分类器，可以对特征质量进行去除研究。)

受此启发，我们开发了一种延迟重新平衡训练程序（算法 1），
该程序首先使用具有 LDAM 损失的 vanilla ERM 进行训练，
然后对学习率进行退火，
然后以较小的学习率部署重新加权的 LDAM 损失。
根据经验，第一阶段的训练导致第二阶段训练的良好初始化，并带有重新加权的损失。 由于损失是非凸的，并且第二阶段的学习率相对较小，因此第二阶段不会将权重移动很远。 有趣的是，通过我们的 LDAM 损失和延迟重新平衡训练，vanilla 重新加权方案（通过每个类中示例数量的倒数重新加权）与之前工作中引入的重新加权方案一样有效[ 崔等，2019]。 我们还发现，通过我们的重新加权方案和 LDAM，我们对提前停止的敏感度低于 [Cui et al., 2019]。

4 Experiments

我们评估算法在人工创建版本的IMDB审查(马斯河et al ., 2011), CIFAR-10, cifar - 100 (Krizhevsky和辛顿,2009)和小ImageNet (Russakovsky et al ., 2015年,锡)和可控度数据的不平衡,以及现实世界的大规模的不平衡数据集,iNaturalist 2018 (V角et al ., 2018)。我们的核心算法是使用PyTorch开发的[Paszke et al.， 2017]。

baseline基线。(1)经验风险最小化(ERM)损失:所有的样本具有相同的权重;默认情况下，我们使用标准的交叉熵损失。(2)重新加权(reweighting, RW):我们将每个样本按其所属类的样本量的倒数重新加权，然后重新归一化，使每个小批量的权重平均为1。(3)重抽样(RS):每个样本的抽样概率与其类的样本量成反比。(4) CB [Cui et al.， 2019]:根据每个类中有效样本数的倒数对样本进行重加权或重采样，定义为(1 - βni)/(1 - β)，而不是类频率的倒数。这个想法可以与重加权或重采样相结合。(5) Focal:我们使用最近提出的Focal loss [Lin et al.， 2017]作为另一个基线。(6) SGD计划:SGD是指学习率在某一阶段衰减为常数的标准计划;我们使用标准的学习率衰减计划。

我们提出的算法和变体。我们测试我们提出的下列技术的组合。
(1) DRW和DRS:在提出的训练算法1之后，我们使用标准的ERM优化计划直到最后一个学习率衰减，然后在第二阶段采用重加权或重采样进行优化。
(2) LDAM:第3.2节中所述的基于标签分布的边际损失。

当这两种方法可以组合时，我们将用中间的破折号作为缩写连接首字母缩略词。我们提出的主要算法是LDAM-DRW。有关更多的实施细节，请参阅B部分。

4.1 Experimental results on IMDB review dataset IMDB综述数据集上的实验结果

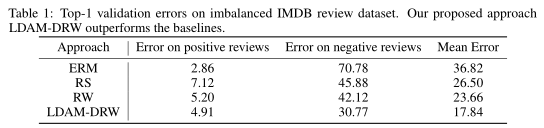
IMDB评论数据集由50000个用于二元情感分类的电影评论组成[Maas等人，2011]。原始数据集包含均匀分布的正面和负面评论。我们手动创建了一个不平衡的训练集，删除了90%的负面评论。我们用Adam优化器训练了一个两层双向LSTM [Kingma and Ba, 2014]。结果见表1。

表一，不平衡IMDB审查数据集的前1位验证错误。我们提出的LDAM-DRW方法优于基线。

4.2 Experimental results on CIFAR CIFAR实验结果

CIFAR-10和CIFAR-100不平衡。CIFAR-10和CIFAR-100的原始版本包含了5万张32×32大小的训练图像和1万张验证图像，分别包含10个和100个类。为了创建它们的非平衡版本，我们减少每个类的训练示例数量，并保持验证集不变。为了确保我们的方法适用于各种情况，我们考虑了两种类型的不平衡:长尾不平衡[Cui等人，2019]和步长不平衡[Buda等人，2018]。我们用不平衡比率ρ表示最频繁类和最不频繁类的样本容量之比，即ρ = maxi{ni}/mini{ni}。长尾不平衡在不同类别的样本中呈指数衰减。对于步长不平衡设置，所有的少数班都有相同的样本量，所有的频繁班也是如此。这就明确了少数班和频繁班的区别，这对于消融研究尤其有用。我们进一步将少数群体的比例定义为µ。默认情况下，我们将所有实验的µ= 0.5。

我们在表2中报告了不平衡版本CIFAR-10和CIFAR-100不同方法的前1位验证误差。我们提出的方法是LDAM-DRW，但我们也包括两种技术的各种组合，以及消融研究的其他损失和训练计划。
表2:ResNet-32对不平衡CIFAR-10和CIFAR-100的Top-1验证误差。我们的两种技术，LDAM-DRW的结合，实现了最佳的性能，并且当与其他损失或计划结合时，每一种技术单独都是有益的。

我们首先表明，提出的标签分布感知边缘交叉熵损失优于纯交叉熵损失和它的变体之一，为不平衡的数据，焦点损失，而没有数据平衡学习计划应用。我们还证明，我们的整个管道大大优于以往的艺术水平。为了进一步证明所提出的LDAM损耗是必要的，我们在交叉熵损耗和铰链损耗的设置下，将其与所有类别的均匀边界正则化进行了比较。我们用M-DRW表示采用均匀裕度交叉熵损失[Wang et al.， 2018a]替代LDAM的算法，即:方程(13)中的∆j被选择为一个不依赖于类别j的调谐常数。铰链损耗(HG)在100个类别中存在优化问题，因此我们仅使用CIFAR-10限制其实验设置。

不平衡但已知的测试标签分布:我们还在测试标签分布已知但不均匀的情况下测试算法的扩展性能。详情请参阅C.5节。

4.3 Visual recognition on iNaturalist 2018 and imbalanced Tiny ImageNet iNaturalist 2018的视觉识别和不平衡的Tiny ImageNet

在大规模非平衡数据集上进一步验证了该方法的有效性。iNatualist物种分类和检测数据集[V an Horn et al.， 2018]是一个真实世界的大规模不平衡数据集，在其2018年版本中有437,513张训练图像，共8142个类。我们在实验中采用官方的训练和验证划分。训练数据集具有长尾标签分布，验证集具有平衡的标签分布。我们使用ResNet-50作为iNaturalist 2018所有实验的骨干网络。表3总结了iNaturalist 2018的前1名验证错误。值得注意的是，在top-1错误方面，我们的完整流水线能够比ERM基线高出10.86%，比之前的技术水平高出6.88%。关于不平衡微小图像网的结果，请参阅附录C.2。

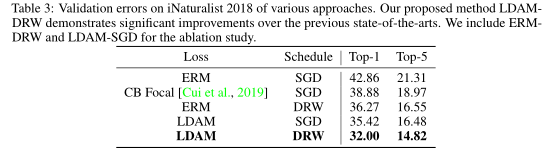
表3:iNaturalist 2018各种方法的V验证错误。我们提出的LDAMDRW方法比以前的先进技术有了显著的改进。我们将ERMDRW和LDAM-SGD纳入消融研究。

4.4 Ablation study 消融实验

对少数类的综合评价。为了更好地理解我们算法的改进，我们在图2中显示了不平衡CIFAR-10上不同方法的每类错误。请参阅标题讨论。

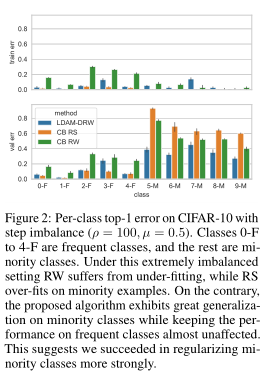
图2:阶跃不平衡(ρ = 100，µ= 0.5)的CIFAR-10的每类top-1误差。0-F班到4-F班是常见班，其余班是少数班。在这种极不平衡的环境下，RW存在拟合不足的问题，而RS在少数例子中则存在过度拟合的问题。相反，该算法在少数类上具有很好的泛化性，而在频繁类上的性能几乎不受影响。这表明，我们成功地使少数民族阶级更加规范化。

评估延迟的重新平衡计划。在图3中，我们将延迟再平衡计划的学习曲线与其他基线进行了比较。节C.3在图6中,我们进一步表明,即使在第一阶段ERM稍差或类似的平衡测试误差RW和RS相比,事实上的特性(倒数层激活)学习ERM由RW和RS。这比同意我们的直觉DRW的第二阶段,从更好的特征开始，调整决策边界，局部微调特征。

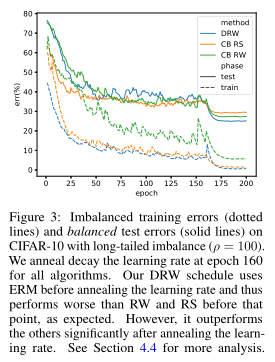
图3:长尾不平衡(ρ = 100) CIFAR-10上的不平衡训练误差(虚线)和平衡测试误差(实线)。我们对所有算法在历元160处的学习率进行了退火衰减。我们的DRW计划在退火学习率之前使用ERM，因此在这一点之前的表现比RW和RS差，正如预期的那样。但在对学习率进行退火处理后，该算法的学习效果显著优于其他算法。更多分析请参见4.4节。

5 Conclusion

我们提出了两种在不平衡数据集上进行训练的方法，标签分布感知边际损失(LDAM)和延迟重加权(DRW)训练计划。我们的方法在各种基准视觉任务上取得了显著的性能改善。此外，我们通过证明LDAM优化了一个均匀标签泛化误差界，从而提供了理论上的合理证明。对于DRW，我们认为推迟重权可以让模型避免重权或重采样相关的缺点，直到它学习到一个良好的初始表示(参见图3和图6中的一些分析)。然而，DRW成功的精确解释在理论上并不完全清楚。我们把这个作为未来工作的方向。

丰田研究所(“TRI”)提供资金和计算资源，以协助作者的研究，但这篇文章仅反映其作者的意见和结论，而不是TRI或任何其他丰田实体。我们感谢梁伯希和谢国忠在这项工作的各个阶段所作的有益讨论。