素材巴巴 > 程序开发 >

多传感器融合 | 一文梳理Allan方差的相关概念

程序开发 2023-09-08 22:48:05

作者 | Zeal  编辑 | 自动驾驶与AI

点击下方卡片，关注“自动驾驶之心”公众号

ADAS巨卷干货，即可获取

点击进入→自动驾驶之心【多传感器融合】技术交流群

后台回复【多传感器标定】获取Lidar/Camera/Radar/IMU等传感器在线离线标定论文！

作者｜Zeal

编辑｜自动驾驶与AI

前言

原本以为Allan方差应该是一个简单的方差计算方法，但是经过两天的各种探索和资料学习，发现这玩意的原理远比想象中的复杂。详细的公式推导需要设计到随机信号的频谱分析、IMU各种误差模型等内容。并且，Allan方差一开始用来分析原子钟晶体振荡频率的误差分析，后续这种分析方法被用到IMU的误差分析，并且IEEE也制订了相应标准（见参考资料1），这一系列的发展过程其实很长，同时也有不同的定义。以上种种，让读者放弃了摸清Allan方差的详细来龙去脉和公式推导，毕竟，工程师和数学家还是有区别的……但是关于Allan方差的解释和应用网上的博文也都不够全面，单看某一篇文章很难获取对Allan方差的直观理解（没有找到一篇很好的文章能够说明Allan方差的定义和双对数曲线不同斜率段对应的噪声项是怎么来的）。

本文对以下内容做了梳理：

  1. IMU的噪声项及其含义

  2. Allan方差的定义和推导

  3. 对陀螺仪的数据计算Allan方差的方法

  4. Allan方差双对数曲线的含义和分析

  5. 关键概念解读

PS: 笔者水平有限，本文只是笔者对Allan方差学习的总结，并不是一篇严格的理论推导文章

惯性测量单元（IMU）误差项

这部分可以参考参考资料2

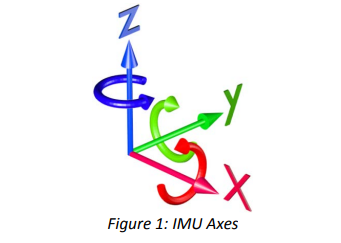0f58855202d12566507b11480158e267.pngIMU模型

IMU的输出可以看上图，典型的六轴IMU输出三个轴的加速度和三个轴的角速度。对加速度做积分可以得到速度、再做一次积分可以得到位移；对角速度积分可以得到角度。

电子器件输出都会有误差，又叫噪声。IMU的噪声项主要有以下几种：

f239bb322e9d40cd2d2e9516ffd70c11.png

IMU误差示意图

  1. 零偏（Bias），单位deg/hr,m/s^2零偏这个词似乎不太准确，因为在非零输出时也会有偏差。如果把IMU的输出当作一个遵循高斯分布的随机信号，在静止时该随机信号的均值应该是零，但是由于bias，该均值并不是0。见上面的IMU误差示意图可以较好地理解。要注意的是零偏是会随着时间改变的，因此在很多卡尔曼滤波模型中会把Bias当作一个状态量。

  2. 零偏可重复性（Bias Repeatability），单位deg/hr,m/s^2每次上电零偏的稳定程度。

  3. 零偏稳定性（Bias Stability），单位deg/hr/hr,m/s^2/hr有时也叫零偏不稳定性（Bias Instability）。描述零偏的稳定程度，也可以理解为零偏的噪声。（有些文章也会叫做零偏的角度随机游走）。

  4. 比例因子（Scale Factor） 比如比例因子是1.2,那么当真值是10m/s^2的时候，IMU的输出可能是12m/s^2。

  5. 角度随机游走（ARW:Angle Random Walk），单位：,这是一个比较难理解的量，实际上笔者也没法完全理解。简单理解就是当信号叠加上一个白噪声之后，对该信号的积分就包含了白噪声的积分，白噪声的积分不再是一个白噪声，而是一个马尔科夫模型，也就是此时的噪声是上一时刻的噪声加上一个白噪声。那么放在这里，对于陀螺仪的输出（角速度）一般是用来做积分得到角度，那么角速度的白噪声的积分就会得到角度的偏差，因此叫做角度随机游走。有时候角度随机游走的值又叫做白噪声强度，比如在kalibr:IMU-Noise-Model中就有这样的描述：

White Noise Terms: The parameters for the "white noise" processes are often specified in the datasheet of the sensor manufacturer. A bit misleading, they are commonly denoted as angular random walk in case of the gyro, and velocity random walk for the accel

  1. 速率随机游走（RRW:Rate Random Walk） 与角度随机游走类似，速率随机游走可以看作是角加速度的误差积分导致的角速度的误差。速率随机游走对应的是陀螺仪在长时间下才会发生改变的误差项，因此可以用来近似当作Bias使用。在kalibr:IMU-Noise-Model中使用速率随机游走系数当作零偏参数。

角度随机游走（ARW:Angle Random Walk）v.s. 角速率随机游走（ARRW）

这个很容易弄混淆的一个概念。对应到加速度计上应该叫速度随机游走和加速度随机游走。因为讲解Allan方差的时候一般会以陀螺仪为示例，因此在文中可能只出现角度随机游走和角速率随机游走。角速率随机游走又会被简写成速率随机游走，比如参考资料1的IEEE标准。下面这段百度百科的描述反而清晰：

角速率传感器的性能参数中包含角度随机游走（ARW）和角速率随机游走（ARRW），前者反映了角速率信号中白噪声的特性，积分后表现为角度随机游走；后者为角速率本身的随机游走，可认为是角加速度白噪声的积分结果。

Allan方差

Allan方差又叫阿伦方差，可以用Allan方差用来描述物理器件的不同噪声参数。Allan方差相比于普通的方差具有更好的描述长时间误差的优势（具体也不太清楚）。Allan方差现在好像基本被用来当作IMU噪声标定的标准方法了。

数据方差

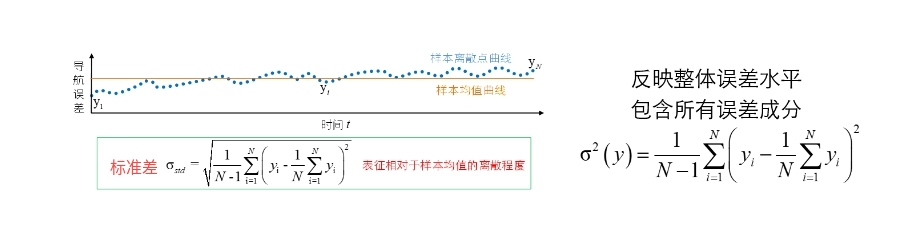
1acb6a8d1aef5ebc5f585c2b34de0aa4.png

（上图引用自新手入门系列3——Allan方差分析方法的直观理解）

系数使得这样计算出来的方差是数据方差的无偏估计（概率统计原理）。

对不同时间尺度上的误差刻画

上面的数据方差计算方法对数据的整个序列计算误差水平，无法细分出不同时间尺度上的误差波动情况。为了能够刻画不同时间周期下数据的波动情况，我们可以先对数据分块，对每块数据取平均作为该块数据的代表。假设原始数据的采样时间是，每3个数据分成一块，则每块的间隔时间。分块之后，我们再将个数据块计算方差，最后求这个方差的数学期望，作为我们最后的方差

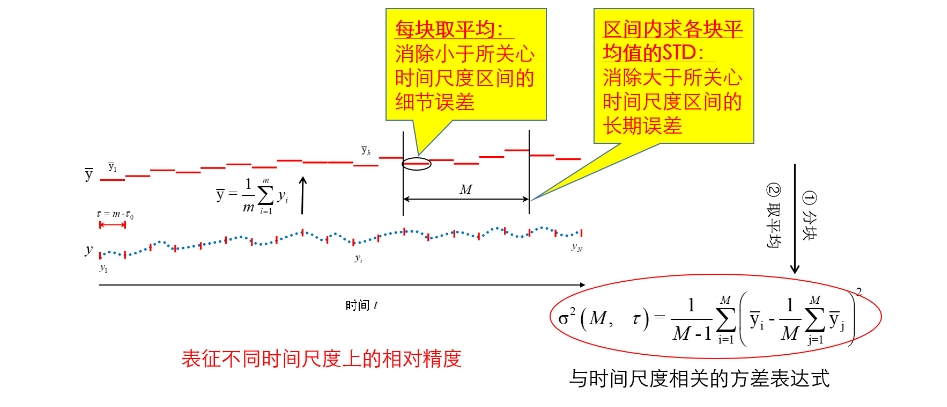
f395245cab2a834d5843cf64aa607c1b.png

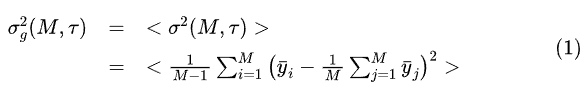
30fa4025355346996296484a98be6a11.png

上式中表示求统计平均（期望）

Allan方差定义

Allan方差是上述通用样本方差分析在时的一个特例，也就是在公式（1）中令

注意，Allan方差是的函数

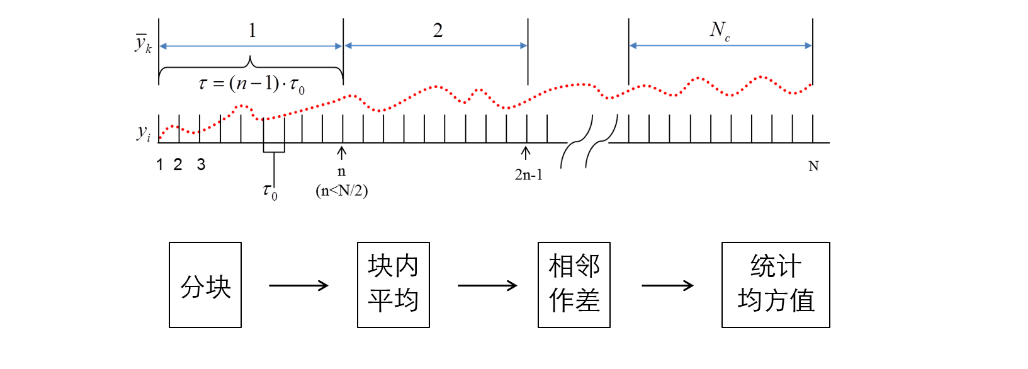
a655820764b220fe5945dbf38757d86f.png

角速度的Allan方差计算

这里只推导一种方式，根据IEEE Standard

令陀螺仪的角度输出为，则角度为

对于离散时间形式，时间点。其中是陀螺仪的输出时间间隔，为总体样本数量。则，在时间段到之间，角速度的平均值是：

其中

将公式（3）带入上文Allan方差的定义公式（2）中可以得到：

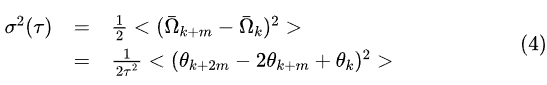
19188dd98d3a3d63245915e7b8f8846e.png

将公式（4）的期望代替为在整个数据样本（数量为N）上求平均，可以得到如下形式

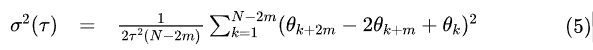
081d7972235ea56f653bb5730d5f07e4.png

重叠分段法计算Allan方差

这部分主要参考：Allan Variance: Noise Analysis for Gyroscopes在公式（5）中，对每个原始数据作为一段。切割方式有很多种，在图Allan方差定义中，每段数据都不重叠。另一种分割方法是让每段数据都重叠，如下图所示

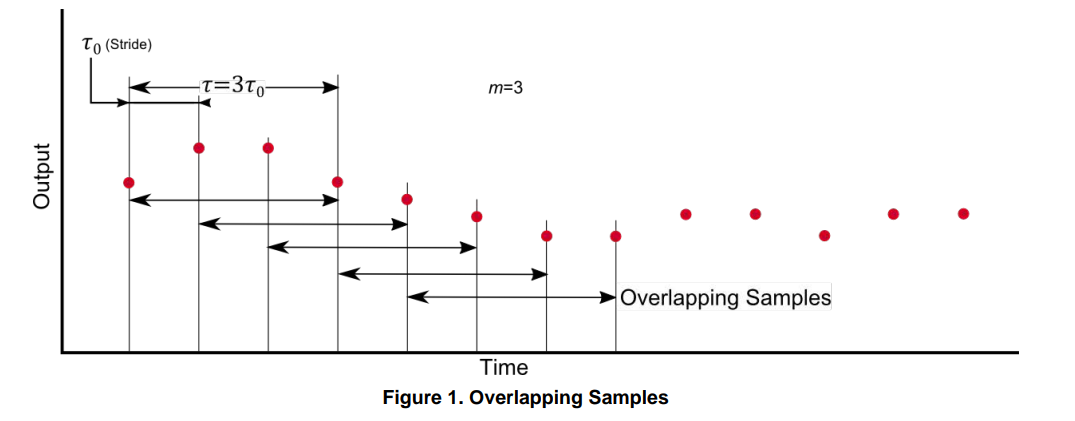
0d9c9e5d5544cecc67d8d3865df14142.png

上图中，也就是每4个原始数据作为一组，组与组之前相差长度。

Allan方差的计算方式与公式（5）保持一致。

Allan方差双对数曲线

根据公式（5），Allan方差是时间周期的函数，我们根据不同的，计算出对应的Allan方差，并将作为x，作为y，画出曲线，如下图：

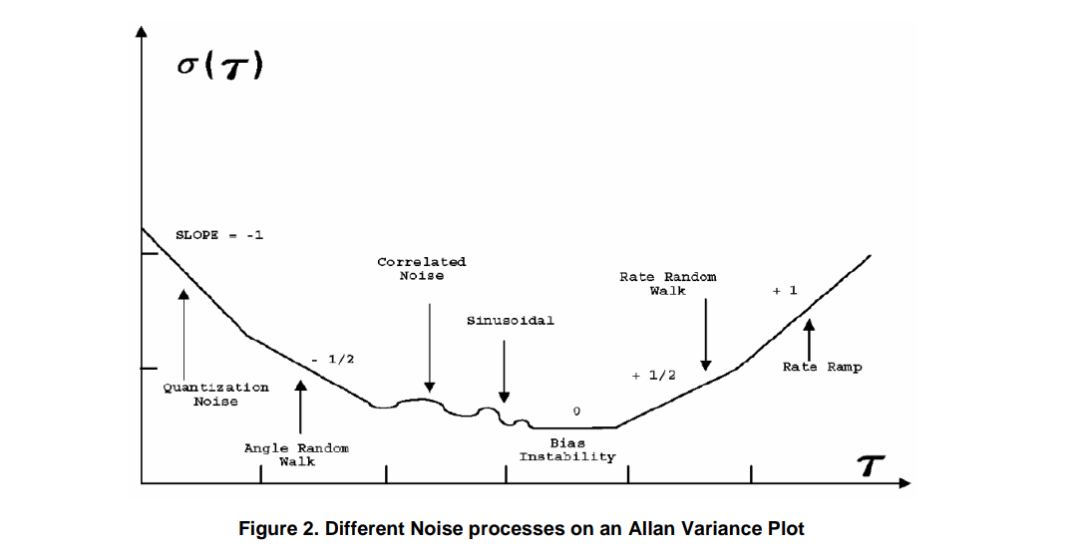
da35bafb5dea3a94c3c5c5f67e9d9bd7.png

注意，y轴是Allan方差的开根，又叫Allan

Allan方差双对数曲线可以用不同斜率的直线拟合，不同斜率部分的直线代表不同的含义。

这里讲述一下如何从双对数曲线分析信号的不同误差成分（以陀螺仪为例）

角度随机游走/白噪声强度

角度随机游走对应到双对数曲线中斜率为的直线，取值可以直接读取处的值。

零偏不稳定性

零偏不稳定性对应双对数曲线中斜率为0的直线，也就是双对数曲线中最小值位置。

速率随机游走

速率随机游走对应双对数曲线中斜率为的直线，取值时取该直线与的交点。

上面三个误差项是我们用得比较多的误差项，画成图如下：

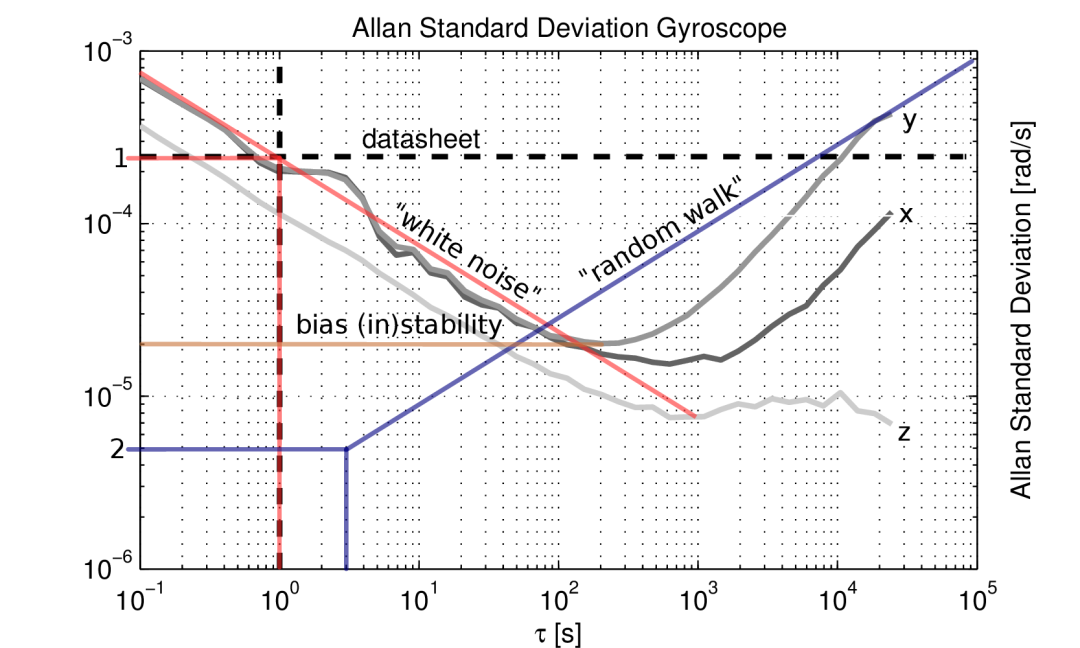
f1f1970920c9a0909b83a2babcd71895.png

为什么不同的斜率对应不同的误差项？？

说实话，笔者对这个部分也是一知半解，说实话，也没有必要完全弄明白，里面涉及到时域信号分析太多基础知识了。这里根据IEEE Standard里一些内容根据自己的理解简单讲述一下。噪声的双边功率谱密度(PSD:Power Sepctral Density)与Allan方差有如下关系：

b779bf4791ef0de9f1ceb5d2fb842e8d.png

上式中可以看作Allan方差是噪声能量经过一个为转移函数的滤波器，这个函数是由Allan方差计算决定的。这个滤波器的带宽跟有关，因此，不同的对应的Allan方差来分析噪声的不同频段特性。

以白噪声为例，其功率谱密度为

3d21c5d96ccb9ce9f080efc65fe6bec4.png

将其带入功率谱密度与Allan方差关系的公式中，并进行公式中的积分，可以得到如下结果:

6e475a0635e8d676e775d6c50e554719.png

对上式  开根后求对数后可以得到

刚好可以得到一条斜率为的直线，且当的时候可以得到。这也对应了上文中从Allan方差双对数曲线中求角度随机游走的方式。

应用重点

不同的IMU建模方式需要不同的系数

强调这一点是因为imu_utils工具标定的输出结果和kalibr的模型要求是不一样的。

在GTSAM中

在GTSAM中使用IMUFactor时需要IMU的几个参数：

  1. IMU零偏Bias的初始值。但是这个参数可以先设置为0,后续逐步更新。（Bias是IMUFactor中的一个变量，会随时间改变）。

  2. IMU加速度（3轴）和陀螺仪（3轴）的噪声参数。

  3. IMU加速度（3轴）和陀螺仪（3轴）的Bias噪声参数。

上面2、3两点的参数可以使用imu_utils的标定结果。

其中第2点对应的是Allan方差双对数曲线（后文详细讲解）中斜率为-1/2的直线与 的交点（IEEE标准）。（可以直接取双对数曲线 处的值，因为"据说"惯性单元在1Hz的时候对应的噪声强度主要由白噪声强度左右。这段话出自kalibr:IMU-Noise-Model，imu_utils也是直接取这一点的值）

This is only true since the noise power in most inertial sensors is dominated by "white noise" at a frequency of approximately 1Hz.

第3点描述的是Bias的不稳定性，有些地方也叫Bias随机游走。这个参数对应的是Bias [In]Stability。Bias Stability可以直接从Allan方差双对数曲线中读出来（后文详解）

之所以GTSAM需要这些参数是因为GTSAM中对IMU的建模方法跟大部分算法相同，都是把IMU的Bias当作状态，认为Bias会随着时间变化而缓慢改变（这也是较为正确的做法）。因此需要标定出Bias的稳定性。

在[kalibr]中在[kalibr]中对IMU的建模是使用下面的公式：

其中代表真值，是Bias，是噪声。因此在[kalibr]中使用角度随机游走系数作为。同时使用角速率随机游走作为。一开始对这点很迷惑，为什么角速率随机游走可以用来作为。后面我在一个issue的回答中得到答案：issues63。[kalibr]对IMU的建模形式实际上是不够准确的，因为这里将当作一个恒定的量求解，实际上这是一个随着时间缓慢变化的量。而角速率随机游走则可以部分用力刻画这一偏差。事实上还是很难理解

单位

First, it is important to realize that Hertz (Hz) is defined as the inverse of seconds, which means that a noise density specification of X°/s/√Hz is exactly equivalent to an angle random walk specification of X°/√s with no conversion necessary. 出自：https://www.vectornav.com/resources/inertial-navigation-primer/specifications--and--error-budgets/specs-imuspecs

参考资料

【1】IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Laser Gyros, AnnexC, IEEE Std 647-1995, 1995

【2】IMU Errors and Their Effects

【3】kalibr:IMU-Noise-Model

【4】imu_utils

【5】新手入门系列3——Allan方差分析方法的直观理解

【6】Allan Variance: Noise Analysis for Gyroscopes

（一）视频课程来了！

自动驾驶之心为大家汇集了毫米波雷达视觉融合、高精地图、BEV感知、传感器标定、传感器部署、自动驾驶协同感知、语义分割、自动驾驶仿真、L4感知、决策规划、轨迹预测等多个方向学习视频，欢迎大家自取（扫码进入学习）

4e978ee66a70a1c85c1f7eb243b05bbd.png

（扫码学习最新视频）

视频官网：www.zdjszx.com

（二）国内首个自动驾驶学习社区

近1000人的交流社区，和20+自动驾驶技术栈学习路线，想要了解更多自动驾驶感知（分类、检测、分割、关键点、车道线、3D目标检测、Occpuancy、多传感器融合、目标跟踪、光流估计、轨迹预测）、自动驾驶定位建图（SLAM、高精地图）、自动驾驶规划控制、领域技术方案、AI模型部署落地实战、行业动态、岗位发布，欢迎扫描下方二维码，加入自动驾驶之心知识星球，这是一个真正有干货的地方，与领域大佬交流入门、学习、工作、跳槽上的各类难题，日常分享论文+代码+视频，期待交流！

76d3fbadfa7c10b14aa96410c6e0b477.jpeg

（三）【自动驾驶之心】全栈技术交流群

自动驾驶之心是首个自动驾驶开发者社区，聚焦目标检测、语义分割、全景分割、实例分割、关键点检测、车道线、目标跟踪、3D目标检测、BEV感知、多传感器融合、SLAM、光流估计、深度估计、轨迹预测、高精地图、NeRF、规划控制、模型部署落地、自动驾驶仿真测试、产品经理、硬件配置、AI求职交流等方向；

8067dc544d2ddf74bc1c78e4b2e4f617.jpeg

添加汽车人助理微信邀请入群

备注：学校/公司+方向+昵称


标签：

上一篇： vs2017和opencv4.1.1的配置 下一篇：

相关文章

    无相关信息
素材巴巴 Copyright © 2013-2021 http://www.sucaibaba.com/. Some Rights Reserved. 备案号：备案中。