python 调用skimage计算灰度共生矩阵并提取GLCM的纹理属性
图像处理库scikits-image已经支持计算灰度共生矩阵和提取GLCM的纹理属性contrast、dissimilarity、homogeneity、ASM、energy、correlation
首先了解一下灰度共生矩阵是什么,下面介绍摘自百度百科。https://baike.baidu.com/item/%E7%81%B0%E5%BA%A6%E5%85%B1%E7%94%9F%E7%9F%A9%E9%98%B5
灰度共生矩阵,指的是一种通过研究灰度的空间相关特性来描述纹理的常用方法。1973年Haralick等人提出了用灰度共生矩阵来描述纹理特征。
由于纹理是由灰度分布在空间位置上反复出现而形成的,因而在图像空间中相隔某距离的两像素之间会存在一定的灰度关系,即图像中灰度的空间相关特性。
取图像(N×N)中任意一点 (x,y)及偏离它的另一点 (x+a,y+b),设该点对的灰度值为 (g1,g2)。令点(x,y) 在整个画面上移动,则会得到各种 (g1,g2)值,设灰度值的级数为 k,则(g1,g2) 的组合共有 k 的平方种。对于整个画面,统计出每一种 (g1,g2)值出现的次数,然后排列成一个方阵,再用(g1,g2) 出现的总次数将它们归一化为出现的概率P(g1,g2) ,这样的方阵称为灰度共生矩阵。距离差分值(a,b) 取不同的数值组合,可以得到不同情况下的联合概率矩阵。(a,b) 取值要根据纹理周期分布的特性来选择,对于较细的纹理,选取(1,0)、(1,1)、(2,0)等小的差分值。
当 a=1,b=0时,像素对是水平的,即0度扫描;当a=0,b=1 时,像素对是垂直的,即90度扫描;当 a=1,b=1时,像素对是右对角线的,即45度扫描;当 a=-1,b=1时,像素对是左对角线,即135度扫描。
这样,两个象素灰度级同时发生的概率,就将 (x,y)的空间坐标转化为“灰度对” (g1,g2)的描述,形成了灰度共生矩阵。
灰度共生矩阵的特征
对比度(contrast)
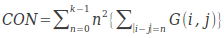
直接反映了某个像素值及其领域像素值的亮度的对比情况。如果偏离对角线的元素有较大值,即图像亮度值变化很快,则CON会有较大取值,这也符合对比度的定义。其中 。反映了图像的清晰度和纹理沟纹深浅的程度。纹理沟纹越深,其对比度越大,视觉效果越清晰;反之,对比度小,则沟纹浅,效果模糊。灰度差即对比度大的象素对越多,这个值越大。灰度公生矩阵中远离对角线的元素值越大,CON越大。
ASM 能量(angular second moment)
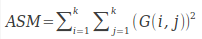
也即每个矩阵元素的平方和。
如果灰度共生矩阵中的值集中在某一块(比如对连续灰度值图像,值集中在对角线;对结构化的图像,值集中在偏离对角线的位置),则ASM有较大值,若G中的值分布较均匀(如噪声严重的图像),则ASM有较小的值。
能量是灰度共生矩阵元素值的平方和,所以也称能量,反映了图像灰度分布均匀程度和纹理粗细度。如果共生矩阵的所有值均相等,则ASM值小;相反,如果其中一些值大而其它值小,则ASM值大。当共生矩阵中元素集中分布时,此时ASM值大。ASM值大表明一种较均一和规则变化的纹理模式。
自相关(correlation)
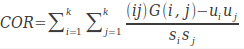
其中
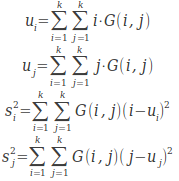
自相关反应了图像纹理的一致性。如果图像中有水平方向纹理,则水平方向矩阵的COR大于其余矩阵的COR值。它度量空间灰度共生矩阵元素在行或列方向上的相似程度,因此,相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时,相关值就大;相反,如果矩阵像元值相差很大则相关值小。
百度百科对应的只有上述三个特征的公式,下面的另外三个特征的公式来自http://tonysyu.github.io/scikit-image/api/skimage.feature.html
相异性(Dissimilarity)
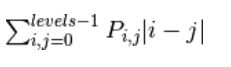
这里的P对应上面的G,levels对应k
计算对比度时,权重随矩阵元素与对角线的距离以指数方式增长,如果改为线性增长,则得到相异性。
同质性/逆差距(Homogeneity)
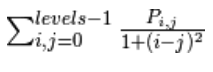
测量图像的局部均匀性,非均匀图像的值较低,均匀图像的值较高。与对比度或相异性相反,同质性的权重随着元素值与对角线的距离而减小,其减小方式是指数形式的。
能量(Energy)
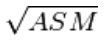
是灰度共生矩阵各元素值的平方和,是对图像纹理的灰度变化稳定程度的度量,反应了图像灰度分布均匀程度和纹理粗细度。能量值大表明当前纹理是一种规则变化较为稳定的纹理。。
好了,下面开始开始实现上面的内容。通过skimage计算灰度共生矩阵并提取上述的六个纹理特征。
scikits-image库提供了两个模块,skimage.feature.greycomatrix(image, …[, …])计算灰度共生矩阵,skimage.feature.greycoprops(P[, prop])计算GLCM的纹理特征。
skimage.feature.greycomatrix(image, distances, angles, levels=256, symmetric=False, normed=False)
参数:
image:array_like of uint8
整数型输入图像。该图像将强制转换为uint8,因此最大值必须小于256。
distances:array_like
像素对距离偏移量列表。
angles:array_like
弧度的像素对角度列表。
级别:整数,可选
输入图像应在[0,levels-1]中包含整数,其中level表示所计数的灰度级数(对于8位图像,通常为256)。最大值为256。
对称:布尔型,可选
如果为True,则输出矩阵P [:,:,d,theta]是对称的。这是通过忽略值对的顺序来实现的,因此在给定偏移量遇到(i,j)时,将同时累积(i,j)和(j,i)。默认值为False。
标准化(归一化):bool,可选
如果为True,则通过除以给定偏移量的累积共现总数,将每个矩阵P [:,:,d,theta]归一化。结果矩阵的元素总和为1。默认值为False。
举个例子演示一下
from skimage.feature import greycomatrix, greycoprops
import numpy as np
image = np.array([[0, 0, 1, 1],
[0, 0, 1, 1],
[0, 2, 2, 2],
[2, 2, 3, 3]], dtype=np.uint8)
#构建了一个44的数组
result = greycomatrix(image, [1], [0, np.pi/2], levels=4)#调用函数
#第一个参数是图像,第二个为距离1,第三个是扫描方向,这里加入了两个方向,0为向右扫描,np.pi/2,90°扫描即垂直扫描;最后一个levels=4即灰度级数。
运行这行代码,会返回一个四维的result结果。即灰度共生直方图,表示形式为p[i,j,d,theta],是灰度级j与灰度级i之间距离为d,角度为θ的情况下出现灰度级j的次数。

生成的result是一个4x4x1x2的数组,因为原始输入的image是一个44的数组,距离d这里只计算了一个,角度计算了两个,所以是4x4x1x2
读取一下result数组
result[:, :, 0, 0] #距离d为1时,扫描角度为0时的result
array([[2, 2, 1, 0],
[0, 2, 0, 0],
[0, 0, 3, 1],
[0, 0, 0, 1]], dtype=uint32)
result[:, :, 0, 1] #距离d为1时,扫描角度为90°时的result
array([[3, 0, 2, 0],
[0, 2, 2, 0],
[0, 0, 1, 2],
[0, 0, 0, 0]], dtype=uint32)
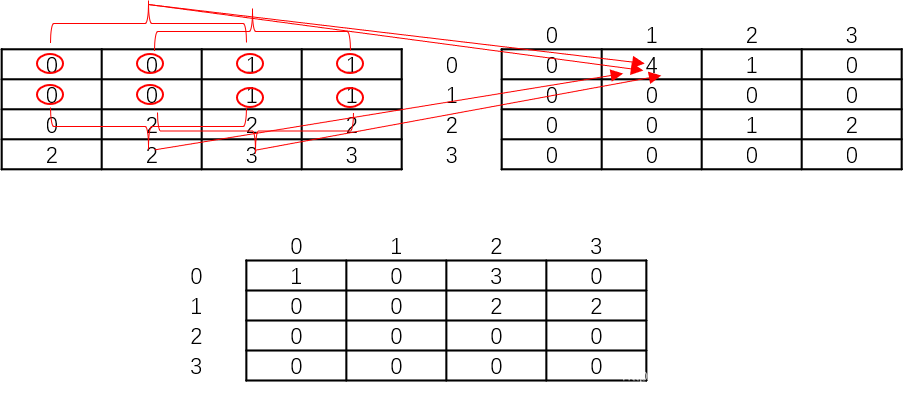
这样一看难以理解,画了个图以便大家理解
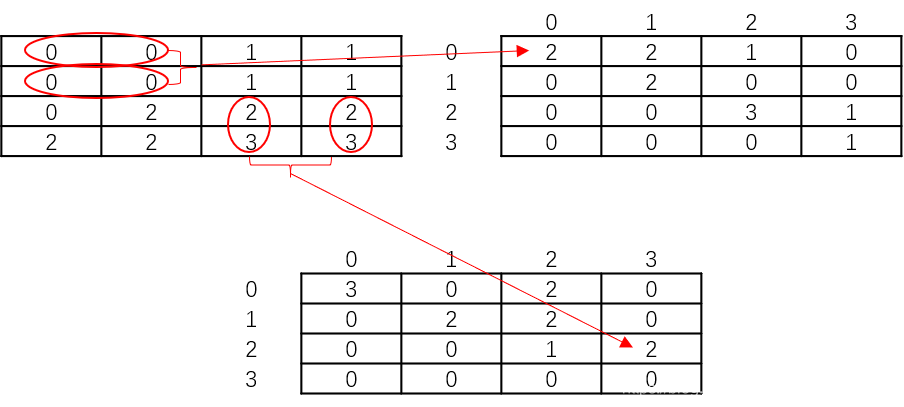
图中右边展示的是0°向右扫描,下边展示的是90°垂直扫描。生成的灰度共生矩阵里面的数是出现次数的统计。
尝试距离为2时的结果
result1 = greycomatrix(image,[2],[0, np.pi/2],levels=4)
result1[:, :, 0, 0]
array([[0, 4, 1, 0],
[0, 0, 0, 0],
[0, 0, 1, 2],
[0, 0, 0, 0]], dtype=uint32)
result1[:, :, 0, 1]
array([[1, 0, 3, 0],
[0, 0, 2, 2],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=uint32)
就画了下0°扫描的(0,1),垂直扫描的示意图就不画了,图已经有点乱了。
result2 = greycomatrix(image,[1,2,3,4],[0, np.pi/2,np.pi/4,np.pi*3/4],levels=4)# 距离为1,2,3,4,扫描方向为0°水平扫描,90°垂直扫描,45°右对角线扫描,135°左对角线扫描。

#读取距离4,左对角线扫描的结果
result2[:, :, 3, 3]
array([[0, 0, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=uint32)
计算6个纹理特征
skimage.feature.greycoprops(P[, prop])
Parameters :
P : ndarray
Input array. P is the grey-level co-occurrence histogram for which to compute the specified property. The value P[i,j,d,theta] is the number of times that grey-level j occurs at a distance d and at an angle theta from grey-level i.
prop : {‘contrast’, ‘dissimilarity’, ‘homogeneity’, ‘energy’, ‘correlation’, ‘ASM’}, optional
The property of the GLCM to compute. The default is ‘contrast’.
Returns :
results : 2-D ndarray
2-dimensional array. results[d, a] is the property ‘prop’ for the d’th distance and the a’th angle.
参数:
P:ndarray
输入数组。P是用于计算指定属性的灰度共生直方图。值 P [i,j,d,θ]是灰度级j在距灰度级i的距离为d且角度为θ的角度出现的次数。
prop:{“对比度”,“相异性”,“同质性”,“能量”,“相关性”,“ ASM”},可选
要计算的GLCM的属性。默认值为“对比度”。
返回值:
结果:2-D ndarray
二维数组。result [d,a]是第d个距离和第a个角度的属性’prop’。
image = np.array([[0, 0, 1, 1],
[0, 0, 1, 1],
[0, 2, 2, 2],
[2, 2, 3, 3]], dtype=np.uint8)
g = greycomatrix(image, [1, 2], [0, np.pi/2], levels=4,
normed=True, symmetric=True)#这里计算灰度共生矩阵,输出的矩阵P [:,:,d,theta]是对称的,并对结果进行了归一化
contrast = greycoprops(g, ‘contrast’)
contrast
array([[0.58333333, 1. ],
[1.25 , 2.75 ]])
dissimilarity = greycoprops(g, ‘dissimilarity’)
dissimilarity
array([[0.41666667, 0.66666667],
[1. , 1.5 ]])
#greycoprops()不能同时计算这六个特征,只能挨个计算。
官方文档见:http://tonysyu.github.io/scikit-image/api/skimage.feature.html
这两天因为任务刚接触这个,做了个整理,不足之处还请谅解。有错误之处还请指正,谢谢。
标签:
相关文章
-
无相关信息
