Opencascade源码学习之模型算法_建模算法介绍
Opencascade源码学习之模型算法_建模算法介绍
介绍
建模算法模块汇集了广泛的拓扑算法用于建模。除了这些工具,你还会发现几何算法。
几何工具
Open CASCADE Technology几何工具提供以下算法:
相交
交集组件用于计算二维或三维几何对象之间的交集:
类Geom2dAPI_InterCurveCurve评估两个几何曲线Geom2d_Curve的交点gp_Pnt2d,也可以计算一个曲线自相交的交点。

在这两种情况下,算法都要求一个两点共同的容差值(Standard_Real)。所有构造函数中使用的默认容差值为1.0e-6。
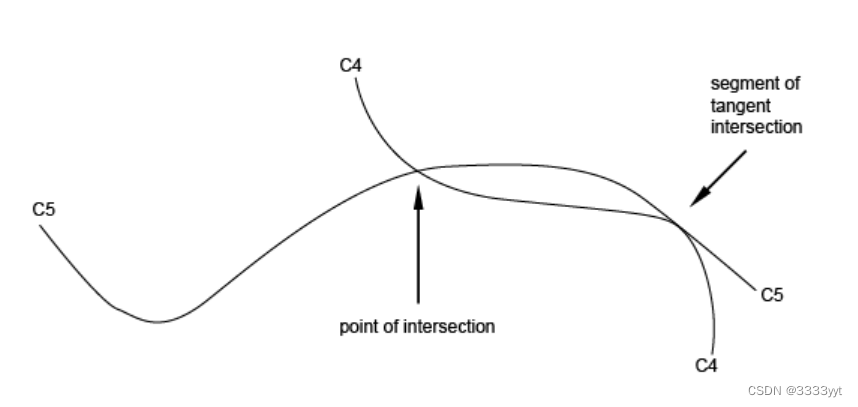
该算法在相交的情况下返回一个点,在相切相交的情况下返回一个段。
两曲线相交
Geom2dApi_Intercurecurve类可以实例化曲线C1和C2的交集。
Geom2dAPI_InterCurveCurve Intersector(C1,C2,tolerance);
或自相交曲线C3
Geom2dAPI_InterCurveCurve Intersector(C3,tolerance);
Standard_Integer N = Intersector.NbPoints();
调用交点的个数
若要选择所需的交点,请在参数中传递整数索引值。
gp_Pnt2d P = Intersector.Point(Index);
要调用交集段的个数,使用
Standard_Integer M = Intersector.NbSegments();
要选择所需的相交段,请在参数中传递整数索引值。
Handle(Geom2d_Curve) Seg1, Seg2;
Intersector.Segment(Index,Seg1,Seg2);
// if intersection of 2 curves
Intersector.Segment(Index,Seg1);
// if self-intersection of a curve
如果您需要访问更广泛的功能,以下方法将返回用于计算交叉点的算法对象:
Geom2dInt_GInter& TheIntersector = Intersector.Intersector();
曲线曲面相交
GeomAPI_IntCS类用于计算曲线和曲面之间的交点。
这个类的实例化如下:
GeomAPI_IntCS Intersector(C, S); 要调用交点的个数,使用:
Standard_Integer nb = Intersector.NbPoints();
gp_Pnt& P = Intersector.Point(Index);
其中Index是1到nb之间的整数,称为交点。
两曲面相交
GeomAPI_IntSS类用于根据给定的公差从Geom_Surface计算两个曲面的相交。
这个类的实例化如下:
GeomAPI_IntSS Intersector(S1, S2, Tolerance);
一旦创建了GeomAPI_IntSS对象,就可以解释它了。
Standard_Integer nb = Intersector. NbLines();
调用交点曲线的个数。
Handle(Geom_Curve) C = Intersector.Line(Index)
其中Index是1到nb之间的整数,称为交点曲线。
插值
插值定律组件提供了函数的定义:y=f(x)。它特别提供了以下定义:
这样的函数可以用来定义,例如,沿形状边缘的圆角的演化规律。
所构建函数的有效性永远不会检查:Law包不知道该函数将用于什么应用程序或用于什么目的。特别是,如果用函数作为圆角的演化规律,重要的是函数总是正的。用户必须对此进行检查。
Geom2dAPI_Interpolate
这个类用于插值一个通过点数组的BSplineCurve。如果在插值点不要求切线,则连续性为C2。如果在该点处要求切线,则连续性为C1。如果要求周期性,曲线是闭合的,连接点将是给出的第一个点。曲线只有C1的连续性。这个类可以实例化如下:
Geom2dAPI_Interpolate
(const Handle_TColgp_HArray1OfPnt2d& Points,
const Standard_Boolean PeriodicFlag,
const Standard_Real Tolerance);
Geom2dAPI_Interpolate Interp(Points, Standard_False, Precision::Confusion());
可以从上面定义的对象调用b样条曲线。
Handle(Geom2d_BSplineCurve) C = Interp.Curve();
注意Handle(Geom2d_BSplineCurve)操作符已经被方法Curve()重新定义。因此,不需要传递Geom2dAPI_Interpolate类型的中间对象的构造,并且下面的语法是正确的。
Handle(Geom2d_BSplineCurve) C = Geom2dAPI_Interpolate(Points, Standard_False, Precision::Confusion());
GeomAPI_Interpolate
这个类可以实例化如下:
GeomAPI_Interpolate
(const Handle_TColgp_HArray1OfPnt& Points,
const Standard_Boolean PeriodicFlag,
const Standard_Real Tolerance);
GeomAPI_Interpolate Interp(Points, Standard_False, Precision::Confusion());
可以从上面定义的对象调用b样条曲线。
Handle(Geom_BSplineCurve) C = Interp.Curve();
注意Handle(Geom_BSplineCurve)操作符已经被Curve()方法重新定义。因此,不需要传递GeomAPI_Interpolate类型的中间对象的构造,并且下面的语法是正确的。
Handle(Geom_BSplineCurve) C = GeomAPI_Interpolate(Points,Standard_False 1.0 e);
边界条件可以用Load方法施加。
GeomAPI_Interpolate AnInterpolator
(Points, Standard_False, 1.0e-5);
AnInterpolator.Load (StartingTangent, EndingTangent);
约束的直线和圆
约束类型
构建二维圆或直线的算法可以用与其他曲线相关的数值或几何约束来描述。
这些约束如下:
例如,这些算法可以很容易地构造一个半径给定的圆,以直线为中心,与另一个圆相切。
实现的算法比直接构造组件提供的用于构建2D圆或线的算法更复杂。
根据解与表示相切约束的圆或直线的相对位置,切线问题的表达式通常会导致几个结果。
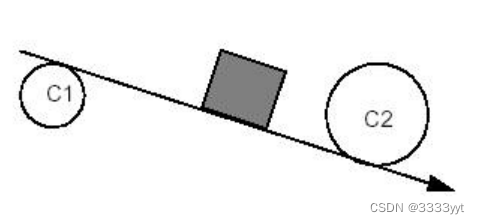
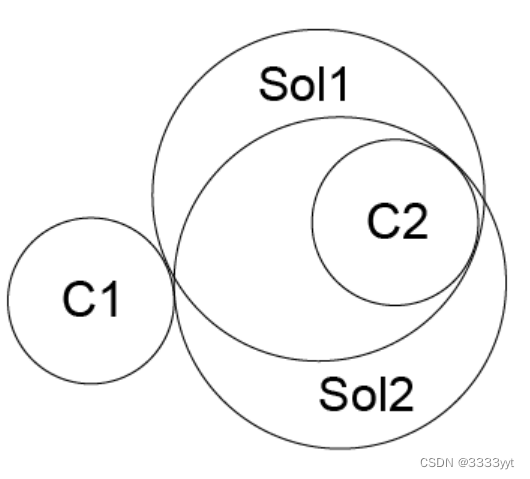
例如,考虑以下一个给定半径的圆(一个小圆)与两个割线圆C1和C2相切的情况:
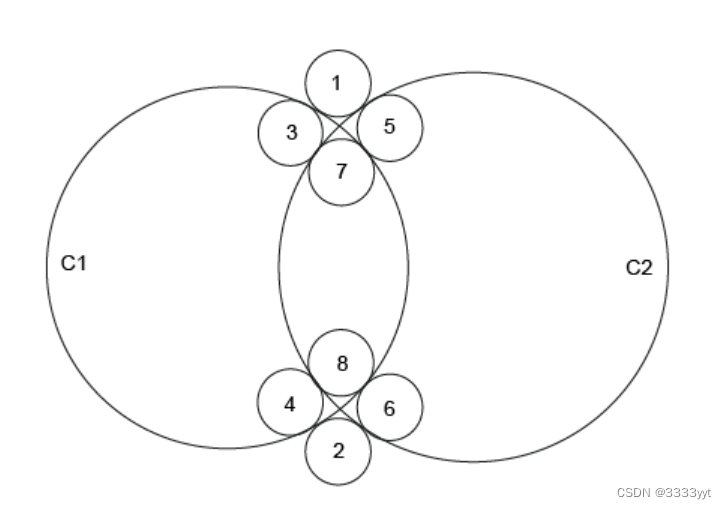
这张图清楚地表明有8种可能的解决方案。
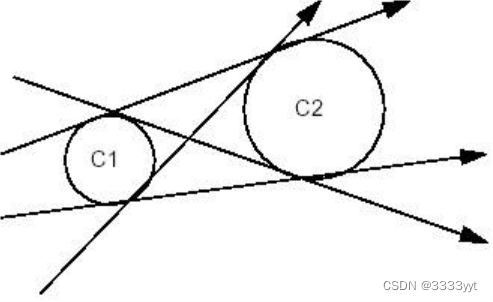
为了限制解的数量,我们可以尝试表示所需解相对于它所相切的圆的相对位置。例如,如果我们指定解决方案在圆圈C1内,在圆圈C2外,则图上只有两个参考3和4的解决方案响应所提出的问题。
这些定义很容易在圆上解释,在圆上很容易识别内部和外部。事实上,对于任何一种曲线,内部都被定义为曲线的左边相对于它的方向。
根据与之相切的曲线来确定解的这种技术,可用于所有通过几何约束构造圆或直线的算法中。使用了四个限定词:
可以使用限定符创建表达式,例如:
GccAna_Circ2d2TanRad Solver(GccEnt::Outside(C1), GccEnt::Enclosing(C2),Rad,Tolerance);
这个表达式找到了所有半径为Rad的圆,它们同时与圆C1和圆C2相切,而C1在外面,C2在里面。
可用的线和圆的类型
以下使用值处理实体创建具有几何约束的二维直线或圆的分析算法是可用的:
外部/内部
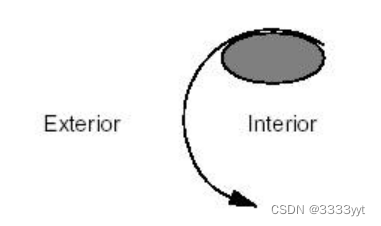
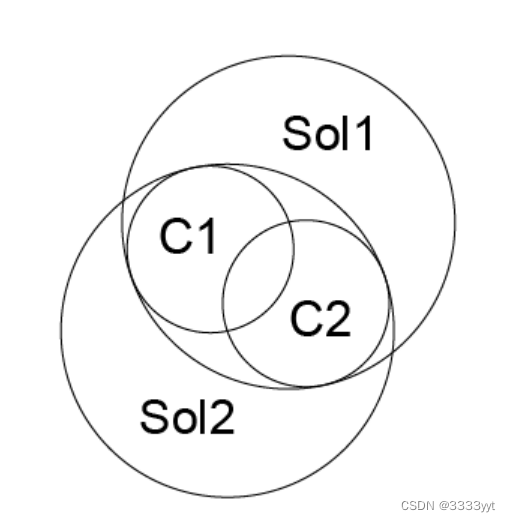
定义一个圆的内部和外部并不难。如下图所示,外部是用双法线的意义来表示的,也就是说,根据穿过圆的意义来表示右边。因此,左侧是内部(或“材料”)。
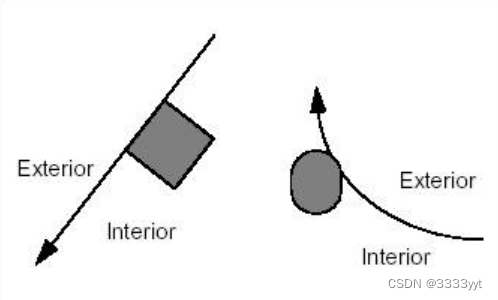
推而广之,将直线或任意开口曲线的内部根据通过方向定义为左侧,如下图所示:
直线的方向
有时有必要事先定义沿着要创建的路线旅行的方向。这种方向将从第一个点到第二个点。
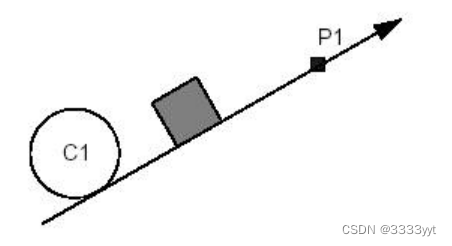
两个圆相切
以下四个图说明了在创建一行时使用限定符的四种情况。第五个显示了如果没有给出限定符的情况下的解决方案。
案例1
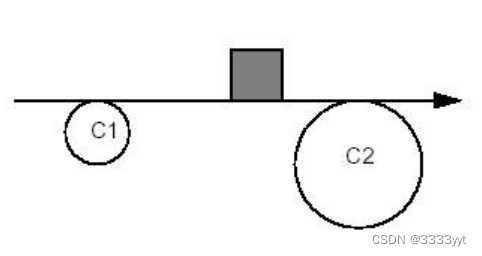
约束:与C1相切和外部。C2的切线和外部。
GccAna_Lin2d2Tan Solver(GccEnt::Outside(C1), GccEnt::Outside(C2), Tolerance);
案例2
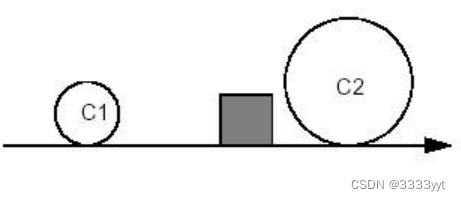
约束:相切且包含C1,相切且包含C2。
GccAna_Lin2d2Tan Solver(GccEnt::Enclosing(C1), GccEnt::Enclosing(C2), Tolerance);
案例3
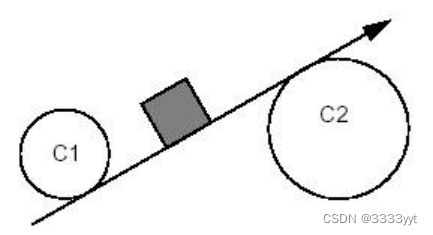
约束:相切且包含C1。C2的正切和外切。
GccAna_Lin2d2Tan Solver(GccEnt::Enclosing(C1), GccEnt::Outside(C2), Tolerance);
案例4
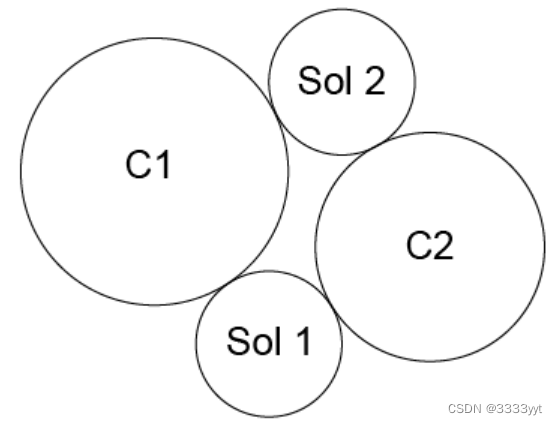
约束:与C1相切且在C1外部,相切且包含C2。
GccAna_Lin2d2Tan Solver(GccEnt::Outside(C1), GccEnt::Enclosing(C2), Tolerance);
案例5
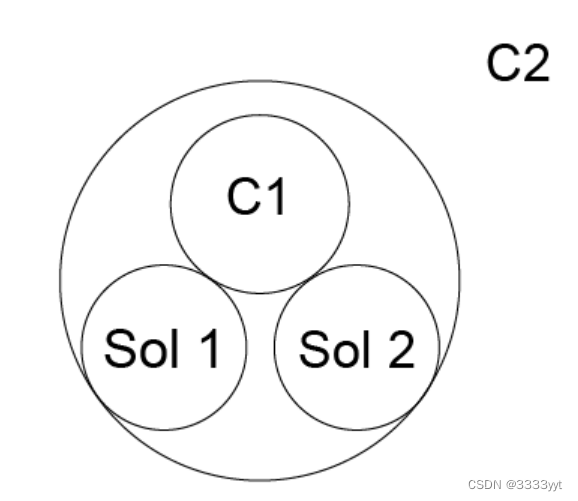
约束条件:与C1相切且未定义。关于C2的正切且未定义。
GccAna_Lin2d2Tan Solver(GccEnt::Unqualified(C1), GccEnt::Unqualified(C2), Tolerance);
给定半径的圆与两个圆相切
下面的四张图显示了在创建圆时使用限定词的四种情况。
案例1
约束:与C1相切且在C1外部。C2的正切和外切。
GccAna_Circ2d2TanRad Solver(GccEnt::Outside(C1), GccEnt::Outside(C2), Rad, Tolerance);
案例2
约束:与C1相切且在C1外部。正切并包含在C2中。
GccAna_Circ2d2TanRad Solver(GccEnt::Outside(C1), GccEnt::Enclosed(C2), Rad, Tolerance);
案例3
约束:与C1相切且在C1外部。相切且包含C2。
GccAna_Circ2d2TanRad Solver(GccEnt::Outside(C1), GccEnt::Enclosing(C2), Rad, Tolerance);
案例4
约束:切线和封闭C1。正切和封闭C2。
GccAna_Circ2d2TanRad Solver(GccEnt::Enclosing(C1), GccEnt::Enclosing(C2), Rad, Tolerance);
案例5
下面的语法将给出所有半径为Rad的圆,它们与C1和C2相切,而不受相对位置的影响:
GccAna_Circ2d2TanRad Solver(GccEnt::Unqualified(C1), GccEnt::Unqualified(C2), Rad,Tolerance);
算法的类型
OCCT实现了几类算法:
对于每一种受约束的直线或圆的几何结构,OCCT提供了两种类型的访问:
所提供的算法计算,对应于与所述几何问题的所有解,除非解是通过迭代算法找到的。
迭代算法只计算一个最接近初始位置的解。它们可以在以下情况下使用:
合格曲线(用于切线参数)由以下方式提供:
GccEnt和Geom2dGcc包也提供了简单的功能,以非常有效的方式构建合格的曲线。
GccAna包还提供了在圆、线或点之间构造等分轨迹的算法。两个几何物体之间的等分轨迹使得它们的每个点与两个几何物体的距离相同。它们通常是曲线,例如GccAna算法中的圆、线或圆锥。每个初等解作为一个初等等分轨迹对象给出(直线,圆,椭圆,双曲线,抛物线),由GccInt包描述。
注:GccAna算法用来定义要求解的几何问题的曲线,是gp包中的二维直线或圆,没有显式参数化。然而,这些线或圆保留隐式参数化,对应于它们在等效的Geom2d对象上的参数化。这种参数化是在这样的曲线上返回参数值时使用的,例如使用函数Tangency1, Tangency2, Tangency3, Intersection2和CenterOn3,这些函数由GccAna或Geom2dGcc包中的构造算法提供。
约束的曲线和曲面
来自约束的曲线和曲面组件将2D和3D几何中使用的高级函数组合在一起,用于:
OPEN CASCADE公司还提供了一种名为Surfaces from Scattered Points的产品,该产品允许从分散的点构建表面。该算法接受或构造一个初始b样条曲面,并寻找其满足约束条件的变形(有限元法)。通过优化的计算方法,该算法可以由超过50万个点构建一个曲面。
SSP产品不随Open CASCADE Technology一起提供,但可以单独购买。
平滑、极小变化的2D曲线
弹性梁曲线起源于造船中应用的传统建模方法,在这种方法中,一根细长的木头,一个车床,被迫在两组钉子之间通过,这样,根据两点,施加在这两点上的力的方向,以及木制车床本身的特性,采取曲线的形式。
保持这些约束要求纵向和横向力都施加到梁上,以补偿其内部弹性。纵向力可以是推或拉,梁可以或可以不允许在这些固定点上滑动。
Batten曲线
类FairCurve_Batten允许生成基于两个参考点上的一个或多个约束定义的平滑曲线。这些包括点,切线角和曲率设置。以下约束顺序可用:
只使用0和1个约束顺序。函数Curve返回结果为2D b样条曲线。
极小变化的曲线
类FairCurve_MinimalVariation允许在每个参考点生成曲率变化最小的曲线。以下约束顺序可用:
约束顺序为0、1和2。该算法最大限度地减少张力,下垂和抽搐能量。
函数Curve返回结果为2D b样条曲线。
如果你想给一条Batten曲线一个特定的长度,使用:
b.SetSlidingFactor(L / b.SlidingOfReference())
其中b是Batten曲线对象的名称
自由滑动通常比受限滑动更美观。然而,当角度大于p/2时,计算可能会失败,因为在这种情况下,长度理论上是无限的。
在其他情况下,当施加滑动且滑动系数过大时,板条可能会坍塌。
构造函数参数Tolerance和NbIterations控制了计算的精确程度和所需的时间。
直纹面
直纹曲面是沿两条曲线的长度绘制一条直线而形成的。
贝塞尔曲面的创建
类GeomFill_BezierCurves允许从连续的Bezier曲线生成一个Bezier曲面。注意,有理贝塞尔曲线可能会出现问题。
B样条曲面的创建
类GeomFill_BSplineCurves允许从连续的b样条曲线生成一个b样条曲面。注意,有理b样条可能会出现问题。
管状曲面的创建
类GeomFill_Pipe允许通过沿着另一条曲线(路径)扫描曲线(截面)来生成管道。结果是一个b样条曲面。
以下类型的结构是可用的:
填充一个轮廓
从一些曲线中创建一个曲面通常很方便,这些曲线将形成定义新曲面的边界。这是通过类GeomFill_ConstrainedFilling完成的,它允许填充由三条或四条曲线以及切线约束定义的轮廓。得到的曲面是一个b样条。
一个恰当的例子是两个圆角的交点。如果一个边缘上的圆角半径与另一个边缘上的圆角半径不同,则不可能将所得表面的所有边缘缝合在一起。这会在你正在构建的物体的整体表面留下一个缺口。
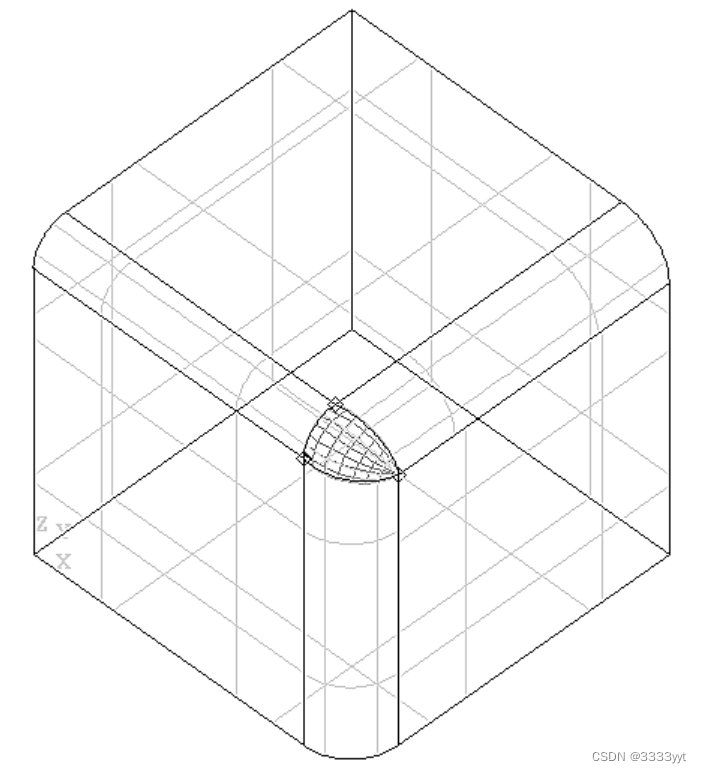
这些算法允许你从两条、三条或四条曲线中填补这个空白。这可以在有约束或没有约束的情况下完成,生成的曲面将是一系列填充样式之一的贝塞尔曲面或b样条曲面。
创建边界
类GeomFill_SimpleBound允许你为要构造的表面定义一个边界。
通过邻面创建边界
类GeomFill_BoundWithSurf允许定义要构造的表面的边界。这个边界已经连接到另一个表面。
填充类型
枚举FillingStyle指定用于构建表面的样式。这些包括:
Plate曲面
在CAD中,经常需要生成没有精确数学定义的曲面,但这些曲面是由各自的约束定义的。这些可以是数学的、技术的或美学的顺序。
从本质上讲,Plate表面是通过变形表面来构造的,使其符合给定数量的曲线或点约束。在下图中,可以看到平面轮廓的四段,以及一个分别作为曲线约束和点约束的点。生成的曲面可以通过使用MakeApprox函数转换为BSpline曲面。
使用变分样条算法构建曲面。它利用薄板在局部机械力作用下变形的原理。如果输入中没有给出,则计算初始曲面。这对应于变形前的板块。然后调用算法计算最终曲面。它寻找满足约束条件并使能量输入最小的解。
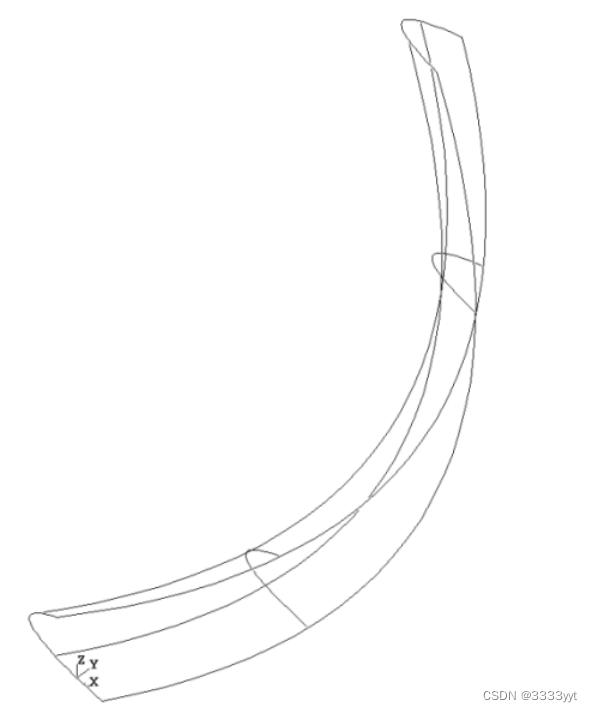
GeomPlate包提供以下服务,用于创建符合曲线和点约束的表面.
定义线框
BuildPlateSurface类允许创建一个框架,根据曲线和点的约束以及公差设置来构建曲面。结果与Surface函数一起返回。
请注意,您不必在构造时指定初始表面。它可以稍后添加,或者,如果没有加载,曲面将自动计算。
定义曲线约束
类CurveConstraint 允许定义曲线作为你想要构建的曲面的约束。
定义点约束
类PointConstraint允许将点定义为您想要构建的曲面的约束
应用Geom_Surface到plate曲面
类Surface允许使用Geom_Surface的方法描述buildplatessurface::Surface返回的Plate曲面对象的特征
拟合Plate曲面为B样条
MakeApprox类允许将一个GeomPlate表面转换为一个Geom_BSplineSurface。
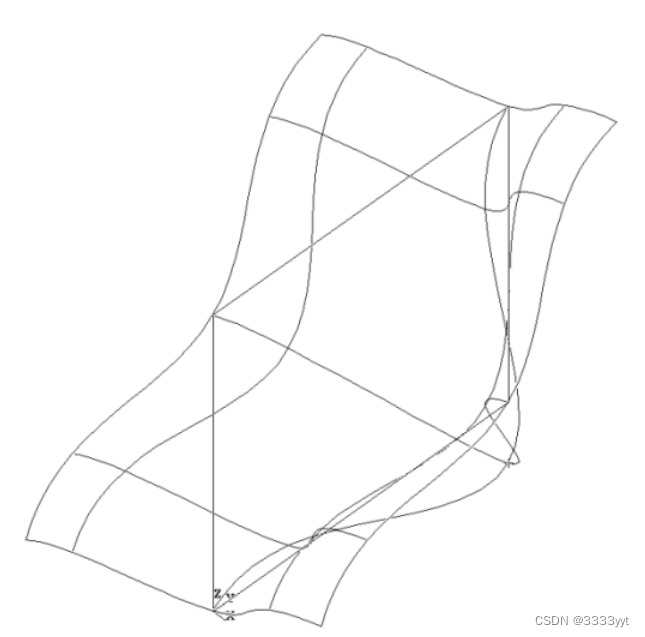
让我们创建一个板表面,并从折线近似为曲线约束和点约束
Standard_Integer NbCurFront=4,
NbPointConstraint=1;
gp_Pnt P1(0.,0.,0.);
gp_Pnt P2(0.,10.,0.);
gp_Pnt P3(0.,10.,10.);
gp_Pnt P4(0.,0.,10.);
gp_Pnt P5(5.,5.,5.);
BRepBuilderAPI_MakePolygon W;
W.Add(P1);
W.Add(P2);
W.Add(P3);
W.Add(P4);
W.Add(P1);
// Initialize a BuildPlateSurface
GeomPlate_BuildPlateSurface BPSurf(3,15,2);
// Create the curve constraints
BRepTools_WireExplorer anExp;
for(anExp.Init(W); anExp.More(); anExp.Next())
{
TopoDS_Edge E = anExp.Current();
Handle(BRepAdaptor_HCurve) C = new
BRepAdaptor_HCurve();
C-ChangeCurve().Initialize(E);
Handle(BRepFill_CurveConstraint) Cont= new
BRepFill_CurveConstraint(C,0);
BPSurf.Add(Cont);
}
// Point constraint
Handle(GeomPlate_PointConstraint) PCont= new
GeomPlate_PointConstraint(P5,0);
BPSurf.Add(PCont);
// Compute the Plate surface
BPSurf.Perform();
// Approximation of the Plate surface
Standard_Integer MaxSeg=9;
Standard_Integer MaxDegree=8;
Standard_Integer CritOrder=0;
Standard_Real dmax,Tol;
Handle(GeomPlate_Surface) PSurf = BPSurf.Surface();
dmax = Max(0.0001,10*BPSurf.G0Error());
Tol=0.0001;
GeomPlate_MakeApprox
Mapp(PSurf,Tol,MaxSeg,MaxDegree,dmax,CritOrder);
Handle (Geom_Surface) Surf (Mapp.Surface());
// create a face corresponding to the approximated Plate
Surface
Standard_Real Umin, Umax, Vmin, Vmax;
PSurf->Bounds( Umin, Umax, Vmin, Vmax);
BRepBuilderAPI_MakeFace MF(Surf,Umin, Umax, Vmin, Vmax);
投影
投影提供下列计算:
–2D点在曲线上的投影
Geom2dAPI_ProjectPointOnCurve允许计算从一个点(gp_Pnt2d)投射到几何曲线(Geom2d_Curve)上的所有法线。计算可能被限制在给定的域内。
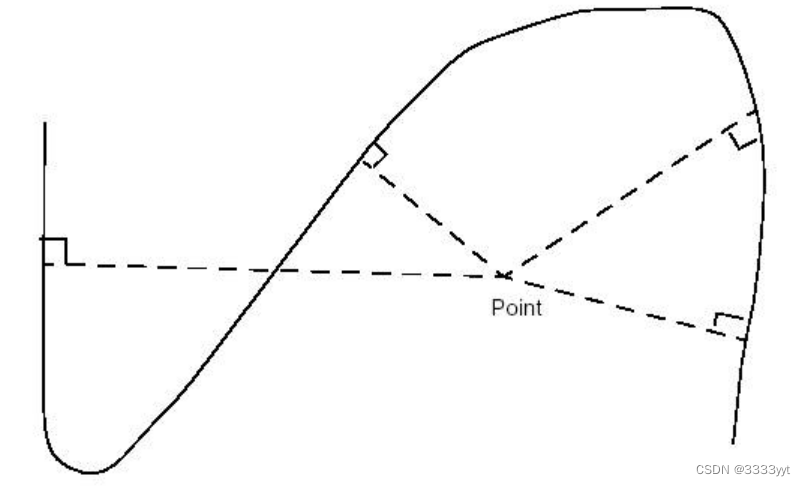
曲线不必是Geom2d_TrimmedCurve。该算法将与继承Geom2d_Curve的任何类一起工作。
类Geom2dAPI_ProjectPointOnCurve可以像下面的例子那样实例化:
gp_Pnt2d P;
Handle(Geom2d_BezierCurve) C = new Geom2d_BezierCurve(args);
Geom2dAPI_ProjectPointOnCurve Projector (P, C);
要将法线的搜索限制在给定域[U1,U2],使用以下构造函数:
Geom2dAPI_ProjectPointOnCurve Projector (P, C, U1, U2);
这样创建了Geom2dAPI_ProjectPointOnCurve对象之后,我们现在可以查询它了。
调用解的点个数
Standard_Integer NumSolutions = Projector.NbPoints();
调用局部解的点
解的索引范围从1到project . nbpoints()。可以找到与给定索引对应的点:
gp_Pnt2d Pn = Projector.Point(Index);
调用参数解的点
对于对应于给定索引的给定点:
Standard_Real U = Projector.Parameter(Index);
这也可以编程为:
Standard_Real U;
Projector.Parameter(Index,U);
调用起止点的距离
我们可以求出初始点到某点的距离,对应给定的Index:
Standard_Real D = Projector.Distance(Index); 调用最近解的点
这个类提供了一个方法来返回离起点最近的解点。该解决方案的访问方式如下:
gp_Pnt2d P1 = Projector.NearestPoint(); 调用参数最近解的点
Standard_Real U = Projector.LowerDistanceParameter(); 调用点到曲线最小距离
Standard_Real D = Projector.LowerDistance(); 重定义操作符
为了找到最接近的解决方案,一些操作已经被重新定义。
Standard_Real()返回从点到曲线的最小距离。
Standard_Real D = Geom2dAPI_ProjectPointOnCurve (P,C);
Standard_Integer()返回解的个数。
Standard_Integer N =
Geom2dAPI_ProjectPointOnCurve (P,C);
gp_Pnt2d()返回最近的解点。
gp_Pnt2d P1 = Geom2dAPI_ProjectPointOnCurve (P,C); 当您只需要最近的点时,使用这些操作符可以使编码更容易。因此:
Geom2dAPI_ProjectPointOnCurve Projector (P, C);
gp_Pnt2d P1 = Projector.NearestPoint();
可以更简洁地写为:
gp_Pnt2d P1 = Geom2dAPI_ProjectPointOnCurve (P,C); 然而,请注意,在第二种情况下,没有创建中间的Geom2dAPI_ProjectPointOnCurve对象,因此不可能访问其他解的点。
访问较底层的函数
如果希望使用Extrema包提供的更广泛的功能,则调用Extrema()方法将返回用于计算极值的算法对象。例如:
Extrema_ExtPC2d& TheExtrema = Projector.Extrema(); –3D点在曲线上的投影
类GeomAPI_ProjectPointOnCurve的实例化如下面的例子:
gp_Pnt P;
Handle(Geom_BezierCurve) C = new Geom_BezierCurve(args);
GeomAPI_ProjectPointOnCurve Projector (P, C);
如果您希望将法线的搜索限制在给定域[U1,U2],请使用以下构造函数:
GeomAPI_ProjectPointOnCurve Projector (P, C, U1, U2);
这样创建了GeomAPI_ProjectPointOnCurve对象之后,您现在可以查询它了。
调用解的点数量
Standard_Integer NumSolutions = Projector.NbPoints();
调用局部解的点
解的索引范围从1到project . nbpoints()。可以找到对应于给定索引的点:
gp_Pnt Pn = Projector.Point(Index);
调用参数解的点
对于对应于给定索引的给定点:
Standard_Real U = Projector.Parameter(Index);
这也可以编程为:
Standard_Real U;
Projector.Parameter(Index,U);
调用起止点的距离
对应于给定索引的起始点到某点的距离为:
Standard_Real D = Projector.Distance(Index);
调用最近解的点
这个类提供了一个方法来返回离起点最近的解点。该解决方案的访问方式如下:
gp_Pnt P1 = Projector.NearestPoint();
调用参数最近解的点
Standard_Real U = Projector.LowerDistanceParameter();
调用点到曲线的最小距离
Standard_Real D = Projector.LowerDistance();
重定义操作符
一些作业者已经被重新定义,以寻找最接近的解决方案。
Standard_Real()返回从点到曲线的最小距离。
Standard_Real D = GeomAPI_ProjectPointOnCurve (P,C);
Standard_Integer()返回解决方案的个数。
Standard_Integer N = GeomAPI_ProjectPointOnCurve (P,C); gp_Pnt2d()返回最近的解点。
gp_Pnt P1 = GeomAPI_ProjectPointOnCurve (P,C);
当您只需要最近的点时,使用这些操作符可以使编码更容易。这样,
GeomAPI_ProjectPointOnCurve Projector (P, C);
gp_Pnt P1 = Projector.NearestPoint();
可以更简洁地写为:
gp_Pnt P1 = GeomAPI_ProjectPointOnCurve (P,C);
然而,在第二种情况下,没有创建中间的GeomAPI_ProjectPointOnCurve对象,并且不可能访问其他解决方案点。
访问较底层的函数
如果希望使用Extrema包提供的更广泛的功能,则调用Extrema()方法将返回用于计算极值的算法对象。例如:
Extrema_ExtPC& TheExtrema = Projector.Extrema();
–点在曲面上的投影
类GeomAPI_ProjectPointOnSurf允许计算从gp_Pnt的一个点投射到Geom_Surface的几何表面的所有法线。
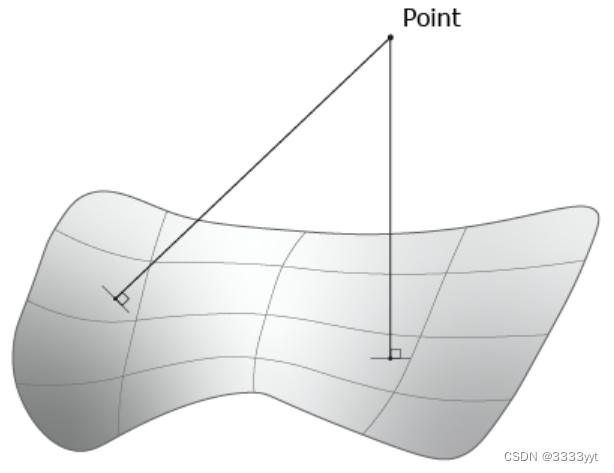
注意,表面不必是Geom_RectangularTrimmedSurface类型。
该算法将适用于继承了Geom_Surface的任何类。
GeomAPI_ProjectPointOnSurf的实例化如下:
gp_Pnt P;
Handle (Geom_Surface) S = new Geom_BezierSurface(args);
GeomAPI_ProjectPointOnSurf Proj (P, S);
要限制在给定矩形域内搜索法线[U1, U2, V1, V2],使用构造函数GeomAPI_ProjectPointOnSurf Proj (P, S, U1, U2, V1, V2)
U1、U2、V1、V2的值均在最大值和最小值范围内,即:
Umin <= U1 < U2 <= Umax
Vmin <= V1 < V2 <= Vmax
这样创建了GeomAPI_ProjectPointOnSurf对象之后,您就可以查询它了。
调用解的点数量
Standard_Integer NumSolutions = Proj.NbPoints();
调用局部解的点
解决方案的索引范围从1到project . nbpoints()。可以找到与给定索引对应的点:
gp_Pnt Pn = Proj.Point(Index);
调用参数解的点
对于对应于给定索引的给定点:
Standard_Real U,V;
Proj.Parameters(Index, U, V);
调用起止点的距离
初始点与给定索引对应点之间的距离为:
Standard_Real D = Projector.Distance(Index);
调用最近距离点
该类提供了一个方法,该方法返回离起始点最近的解决方案点。该解决方案的访问方式如下:
gp_Pnt P1 = Proj.NearestPoint();
调用参数最近解的点
Standard_Real U,V;
Proj.LowerDistanceParameters (U, V);
调用点到曲面的最小距离
Standard_Real D = Proj.LowerDistance(); 重定义操作符
有些操作符已经被重新定义,以帮助您找到最近的解决方案。
Standard_Real()返回从点到表面的最小距离。
Standard_Real D = GeomAPI_ProjectPointOnSurf (P,S); Standard_Integer()返回解的个数。
Standard_Integer N = GeomAPI_ProjectPointOnSurf (P,S); gp_Pnt2d()返回最近的解点。
gp_Pnt P1 = GeomAPI_ProjectPointOnSurf (P,S); 当您只需要最近的点时,使用这些操作符可以使编码更容易。这样,
GeomAPI_ProjectPointOnSurface Proj (P, S);
gp_Pnt P1 = Proj.NearestPoint();
可以更简洁地写为:
gp_Pnt P1 = GeomAPI_ProjectPointOnSurface (P,S);
访问较底层函数
然而,在第二种情况下,没有创建中间的GeomAPI_ProjectPointOnSurf对象,并且不可能访问其他解决方案点。
如果你想使用Extrema包提供的更广泛的功能,调用Extrema()方法将返回用于计算极值的算法对象,如下所示:
Extrema_ExtPS& TheExtrema = Proj.Extrema();
2d和3d曲线切换
To2d和To3d方法用于;
从位于gp_Pln平面上的3d Geom_Curve构建2d曲线,从Geom2d_Curve和gp_Pln平面构建3d曲线。
这些方法的调用方式如下:
Handle(Geom2d_Curve) C2d = GeomAPI::To2d(C3d, Pln);
Handle(Geom_Curve) C3d = GeomAPI::To3d(C2d, Pln);
标准拓扑对象
可以创建如下标准拓扑对象:
它们的构造和修改有两个根类:
点
BRepBuilderAPI_MakeVertex从gp的3D点创建一个新的顶点。
gp_Pnt P(0,0,10);
TopoDS_Vertex V = BRepBuilderAPI_MakeVertex(P);
这个类总是创建一个新的顶点,没有其他的方法。
边
基本边缘构造法
使用BRepBuilderAPI_MakeEdge从曲线和顶点创建。基本方法由一条曲线、两个顶点和两个参数构造一条边。
Handle(Geom_Curve) C = ...; // a curve
TopoDS_Vertex V1 = ...,V2 = ...;// two Vertices
Standard_Real p1 = ..., p2 = ..;// two parameters
TopoDS_Edge E = BRepBuilderAPI_MakeEdge(C,V1,V2,p1,p2);
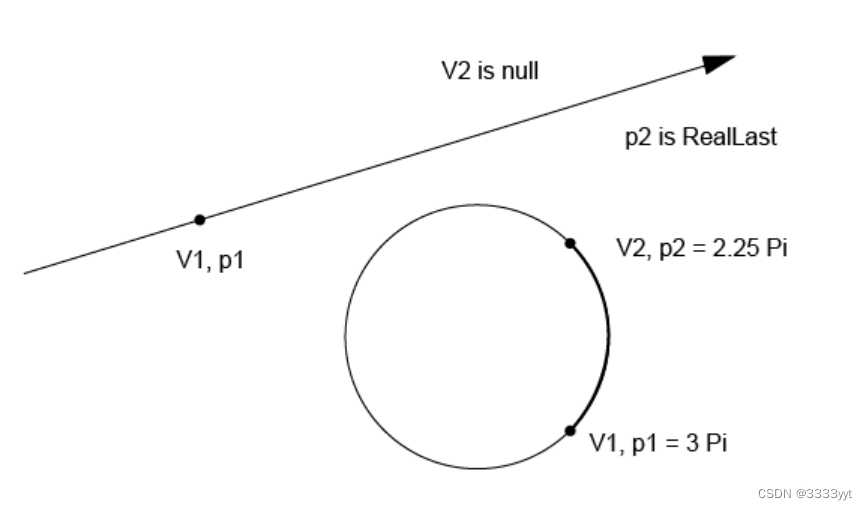
其中C为边的定义域;V1是第一个面向FORWARD的顶点;V2是第二个顶点方向反转;p1和p2是曲线上顶点V1和V2的参数。默认容差与此边相关联。
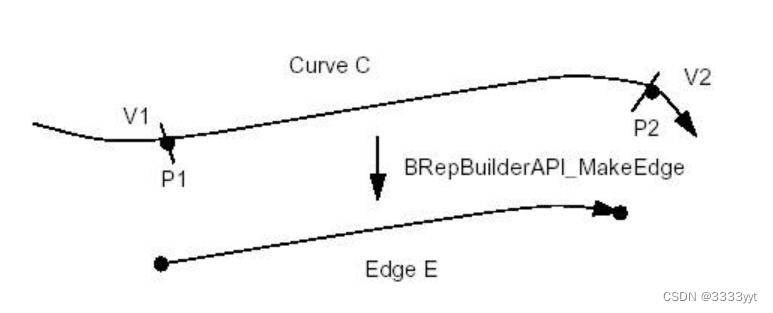
以下规则适用于参数:
曲线
顶点
参数
必须递增且在曲线范围内,即:
C->FirstParameter() <= p1 < p2 <= C->LastParameter()
补充边缘构造方法
在基本边缘构造方法的基础上,还存在补充边缘构造方法。
BRepBuilderAPI_MakeEdge类提供了方法,这些方法都是前一个的简化调用:
因此,从基本结构中衍生出以下五种方法:
Handle(Geom_Curve) C = ...; // a curve
TopoDS_Vertex V1 = ...,V2 = ...;// two Vertices
Standard_Real p1 = ..., p2 = ..;// two parameters
gp_Pnt P1 = ..., P2 = ...;// two points
TopoDS_Edge E;
// project the vertices on the curve
E = BRepBuilderAPI_MakeEdge(C,V1,V2);
// Make vertices from points
E = BRepBuilderAPI_MakeEdge(C,P1,P2,p1,p2);
// Make vertices from points and project them
E = BRepBuilderAPI_MakeEdge(C,P1,P2);
// Computes the points from the parameters
E = BRepBuilderAPI_MakeEdge(C,p1,p2);
// Make an edge from the whole curve
E = BRepBuilderAPI_MakeEdge(C);
还为gp包中的曲线提供了六种方法(上述五种方法和基本方法),以取代来自Geom的曲线。这些方法从Geom中创建相应的曲线,并为以下类实现:
gp_Lin创建了一个Geom_Line, gp_Circ创建了一个Geom_Circle, gp_Elips创建了一个Geom_Ellipse, gp_Hypr创建了一个geom_Hyperbola,gp_Parab创建了一个geom_Parabola。
还有两种方法可以从两个顶点或两个点构造边。这些方法假设曲线是一条直线;顶点或点必须有不同的位置。
TopoDS_Vertex V1 = ...,V2 = ...;// two Vertices
gp_Pnt P1 = ..., P2 = ...;// two points
TopoDS_Edge E; // linear edge from two vertices
E = BRepBuilderAPI_MakeEdge(V1,V2); // linear edge from two points
E = BRepBuilderAPI_MakeEdge(P1,P2);
另一些信息和错误状态
类BRepBuilderAPI_MakeEdge可以提供额外的信息并返回一个错误状态。
如果BRepBuilderAPI_MakeEdge被用作一个类,它可以提供两个顶点。当顶点没有作为参数提供时,这很有用,例如,当从曲线和参数构造边缘时。两个方法Vertex1和Vertex2返回顶点。注意,如果沿相应方向打开,则返回的顶点可以为空。
Error方法返回BRepBuilderAPI_EdgeError枚举的一个项。它可以用来分析IsDone方法返回False时的错误。这些项是:
下面的示例创建一个以维度H、L为中心的矩形,圆角半径为r。边和顶点存储在数组theEdges和theVertices中。我们使用类Array1OfShape(即不是边或顶点的数组)。请看下面的图片。
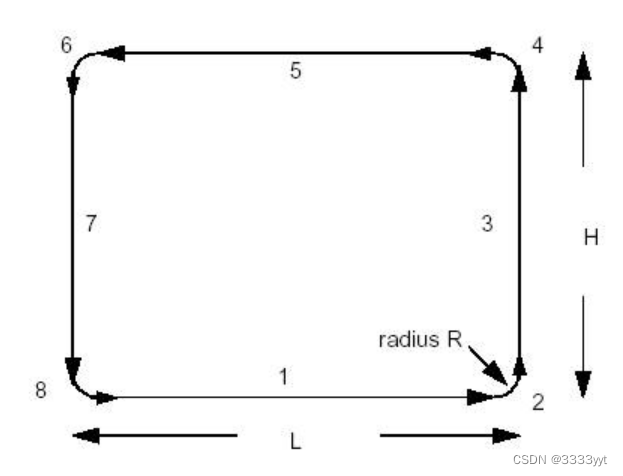
#include
#include
#include
#include
#include
#include
#include // Use MakeArc method to make an edge and two vertices
void MakeArc(Standard_Real x,Standard_Real y,
Standard_Real R,
Standard_Real ang,
TopoDS_Shape& E,
TopoDS_Shape& V1,
TopoDS_Shape& V2)
{
gp_Ax2 Origin = gp::XOY();
gp_Vec Offset(x, y, 0.);
Origin.Translate(Offset);
BRepBuilderAPI_MakeEdge
ME(gp_Circ(Origin,R), ang, ang+PI/2);
E = ME;
V1 = ME.Vertex1();
V2 = ME.Vertex2();
} TopoDS_Wire MakeFilletedRectangle(const Standard_Real H,
const Standard_Real L,
const Standard_Real R)
{
TopTools_Array1OfShape theEdges(1,8);
TopTools_Array1OfShape theVertices(1,8); // First create the circular edges and the vertices
// using the MakeArc function described above.
void MakeArc(Standard_Real, Standard_Real,
Standard_Real, Standard_Real,
TopoDS_Shape&, TopoDS_Shape&, TopoDS_Shape&); Standard_Real x = L/2 - R, y = H/2 - R;
MakeArc(x,-y,R,3.*PI/2.,theEdges(2),theVertices(2),
theVertices(3));
MakeArc(x,y,R,0.,theEdges(4),theVertices(4),
theVertices(5));
MakeArc(-x,y,R,PI/2.,theEdges(6),theVertices(6),
theVertices(7));
MakeArc(-x,-y,R,PI,theEdges(8),theVertices(8),
theVertices(1));
// Create the linear edges
for (Standard_Integer i = 1; i <= 7; i += 2)
{
theEdges(i) = BRepBuilderAPI_MakeEdge
(TopoDS::Vertex(theVertices(i)),TopoDS::Vertex
(theVertices(i+1)));
}
// Create the wire using the BRepBuilderAPI_MakeWire
BRepBuilderAPI_MakeWire MW;
for (i = 1; i <= 8; i++)
{
MW.Add(TopoDS::Edge(theEdges(i)));
}
return MW.Wire();
}
2D边
使用BRepBuilderAPI_MakeEdge2d类从2d曲线在工作平面上制作边缘。工作平面是BRepBuilderAPI包的默认值(参见plane方法)。
BRepBuilderAPI_MakeEdge2d类严格类似于BRepBuilderAPI_MakeEdge,但它使用gp和Geom2d的2D几何形状,而不是3D几何形状。
多边形
BRepBuilderAPI_MakePolygon类用于从顶点或点构建多边形线。点自动更改为顶点在BRepBuilderAPI_MakeEdge。
BRepBuilderAPI_MakePolygon的基本用法是通过使用Add方法添加顶点或点来创建线。在任何时刻,线都可以被提取出来。闭合方法可用于闭合线。在下面的示例中,从点的数组创建一个封闭的线。
#include
#include
#include TopoDS_Wire ClosedPolygon(const TColgp_Array1OfPnt& Points)
{
BRepBuilderAPI_MakePolygon MP;
for(Standard_Integer i=Points.Lower();i=Points.Upper();i++)
{
MP.Add(Points(i));
}
MP.Close();
return MP;
}
为2,3或4个点或顶点提供了快捷方式。这些方法的最后一个参数是布尔值,用来判断多边形是否闭合。默认值为False。
两个例子:
一个由三个顶点组成的封闭三角形的例子:
TopoDS_Wire W = BRepBuilderAPI_MakePolygon(V1,V2,V3,Standard_True); 一个由四个点组成的开放多边形的例子:
TopoDS_Wire W = BRepBuilderAPI_MakePolygon(P1,P2,P3,P4);
BRepBuilderAPI_MakePolygon类维护当前连线。目前的线可以随时抽出,并可以进行处理更长的线。在每个点插入之后,类维护最后创建的边和顶点,它们由Edge、FirstVertex和LastVertex方法返回。
当添加的点或顶点与前一个位置相同时,它不会添加到当前线中,但最近创建的边变为Null。add方法可用于测试此条件。MakePolygon类永远不会引发错误。如果没有添加顶点,则Wire为Null。如果两个顶点在同一位置,则不会创建任何边。
面
使用BRepBuilderAPI_MakeFace类从表面和线创建一个面。底层曲面由曲面和可选参数值构造而成。线可以添加到曲面上。一个平面可以由线构成。面构建后可返回错误状态。
基础面的构造方法
一个面可以由一个表面和四个参数来确定紫外空间的限制。参数是可选的,如果省略它们,则使用表面的自然边界。最多可以用导线创建四个边和顶点。当参数为无穷大时,不会创建任何边。
Handle(Geom_Surface) S = ...; // a surface
Standard_Real umin,umax,vmin,vmax; // parameters
TopoDS_Face F = BRepBuilderAPI_MakeFace(S,umin,umax,vmin,vmax);
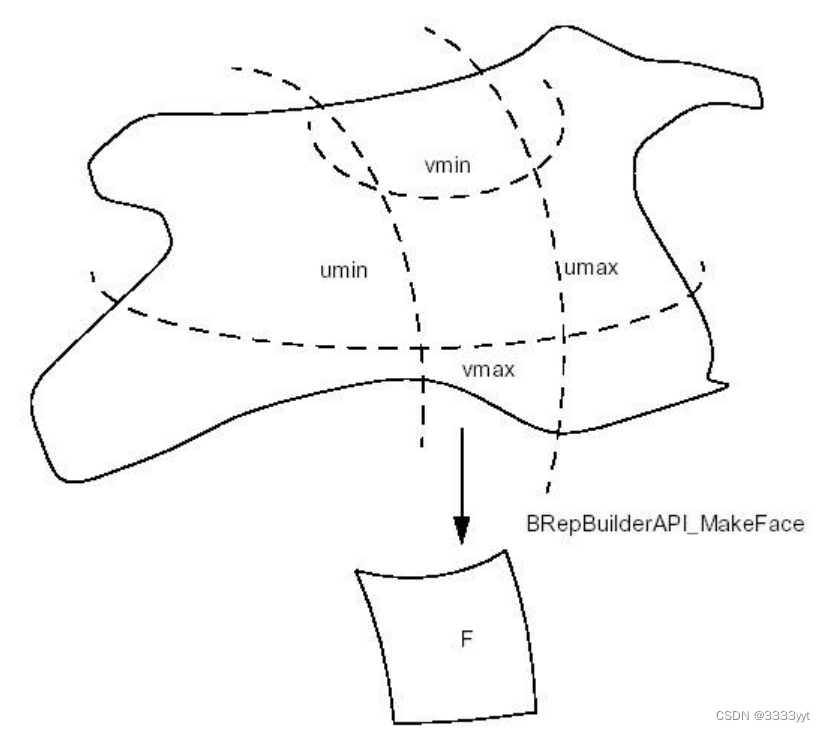
要从曲面的自然边界制作一个面,不需要以下参数:
Handle(Geom_Surface) S = ...; // a surface
TopoDS_Face F = BRepBuilderAPI_MakeFace(S);
参数的约束类似于BRepBuilderAPI_MakeEdge中的约束。
附加面的构造方法
这两种基本构造(从曲面和从曲面和参数)实现了所有gp包表面,它们在相应的Surface中从Geom转换。
一旦创建了一个面,就可以使用Add方法添加一条线。例如,下面的代码创建一个圆柱形表面并添加一条线。
gp_Cylinder C = ..; // a cylinder
TopoDS_Wire W = ...;// a wire
BRepBuilderAPI_MakeFace MF(C);
MF.Add(W);
TopoDS_Face F = MF;
在一个曲面上可以添加一条以上的线,只要它们不相互交叉并且它们只定义曲面上的一个区域。(请注意,此选项未勾选)。
对于一根线,提供了一个简单的语法来从曲面和线构造面。以上几行可以写成:
TopoDS_Face F = BRepBuilderAPI_MakeFace(C,W);
面上的边缘必须有参数化曲线描述。如果线的某条边在曲面上没有参数曲线,则采用投影法计算,而且只能对平面表面进行计算。
只要线定义了平面,就可以仅用线创建平面。例如,要从一组点创建一个平面面,你可以使用BRepBuilderAPI_MakePolygon和BRepBuilderAPI_MakeFace。
#include
#include
#include
#include TopoDS_Face PolygonalFace(const TColgp_Array1OfPnt& thePnts)
{
BRepBuilderAPI_MakePolygon MP;
for(Standard_Integer i=thePnts.Lower();
i<=thePnts.Upper(); i++)
{
MP.Add(thePnts(i));
}
MP.Close();
TopoDS_Face F = BRepBuilderAPI_MakeFace(MP.Wire());
return F;
}
MakeFace的最后一个用途是复制一个现有的面来添加新的线。例如,下面的代码将一个新的线添加到一个面:
TopoDS_Face F = ...; // a face
TopoDS_Wire W = ...; // a wire
F = BRepBuilderAPI_MakeFace(F,W);
要添加多个线,可以创建一个BRepBuilderAPI_MakeFace类的实例,并使用add方法插入面和第一条线以及新线。
错误状态
Error方法返回一个错误状态,这是来自BRepBuilderAPI_FaceError枚举的一个术语。
FaceDone :没有错误发生。
NoFace :不初始化算法;使用了空构造函数。
NotPlanar :没有给出曲面,导线也不是平面的。
CurveProjectionFailed:在曲面的参数空间中没有找到边缘的曲线。
Parametersoutorange:参数umin, umax, vmin, vmax都不在曲面中。
线
线是一个复合形状,不是由一个几何形状,而是由边缘的组装。BRepBuilderAPI_MakeWire类可以从一个或多个边构建一个线,或者将新边连接到现有的线。
最多可直接使用四条边,例如:
TopoDS_Wire W = BRepBuilderAPI_MakeWire(E1,E2,E3,E4);
对于更高或未知数量的边,必须使用Add方法;例如,从一组形状(作为边)构建一条线。
TopTools_Array1OfShapes theEdges;
BRepBuilderAPI_MakeWire MW;
for (Standard_Integer i = theEdge.Lower();
i <= theEdges.Upper(); i++)
MW.Add(TopoDS::Edge(theEdges(i));
TopoDS_Wire W = MW;
类可以用线构造。也可以加一根线。在这种情况下,所有的线的边缘被添加。例如合并两条线:
#include
#include TopoDS_Wire MergeWires (const TopoDS_Wire& W1,
const TopoDS_Wire& W2)
{
BRepBuilderAPI_MakeWire MW(W1);
MW.Add(W2);
return MW;
}
BRepBuilderAPI_MakeWire类将边缘连接到线上。当添加一条新边时,如果它的一个顶点与线共享,则认为它与导线。如果没有共享顶点,则算法搜索位于相同位置的边的顶点和线的顶点(顶点的公差用于测试它们是否具有相同的位置)。如果找到了这样一对顶点,则用线的顶点代替原始顶点复制边缘。边的所有顶点都可以交换为线上的顶点。
BRepBuilderAPI_MakeWire类可以返回添加到连线的最后一条边(edge方法)。如果复制了这条边,它可能与原始边不同。
Error方法返回BRepBuilderAPI_WireError枚举的一个项:
壳
壳是一个复合形状,不是由几何形状,而是由面组装而成。使用BRepBuilderAPI_MakeShell类从一组Faces构建Shell。重要的是,每一个面都应该有必要的连续性。这就是为什么最初的表面被分解成面。
实体
实体是一种复合形状,不是由几何形状构成的,而是由壳的组装而成的。使用BRepBuilderAPI_MakeSolid类从一组shell构建一个Solid。它的使用类似于MakeWire类的使用:将壳添加到实体中,就像在MakeWire中将边缘添加到线中一样。
基础对象
BRepPrimAPI包为构造基础对象提供了一个API(应用程序编程接口),例如:
创建基础对象
盒子
类BRepPrimAPI_MakeBox允许构建一个平行六面体盒子。结果要么是Shell,要么是Solid。有四种方法可以构建一个盒子:
如果使用默认精度,该框在任何维度上都是平坦的,则会引发错误。下面的代码展示了如何创建一个框:
TopoDS_Solid theBox = BRepPrimAPI_MakeBox(10.,20.,30.);
构建方框的四种方法如图所示:
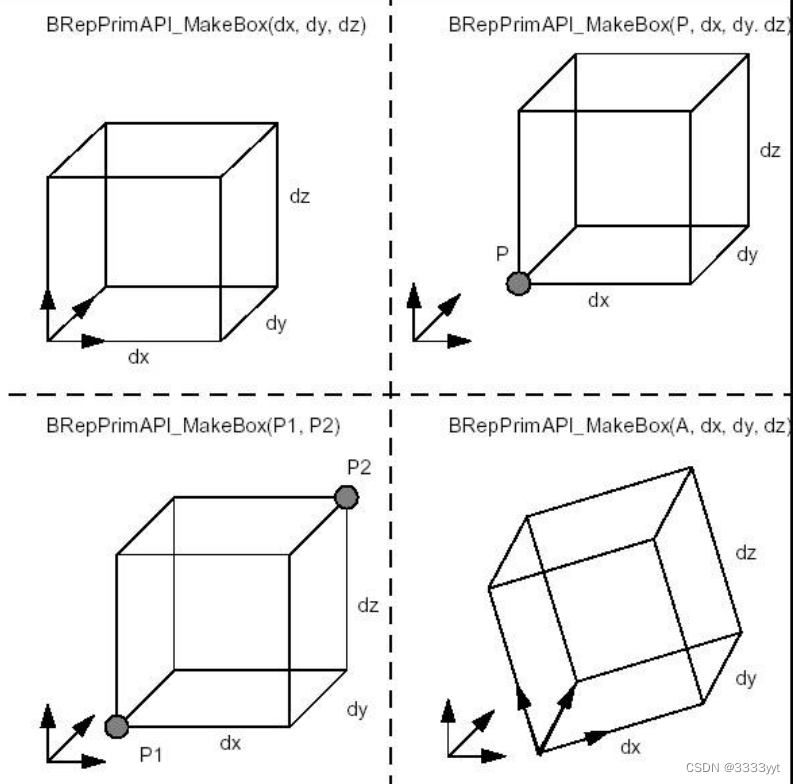
锥体
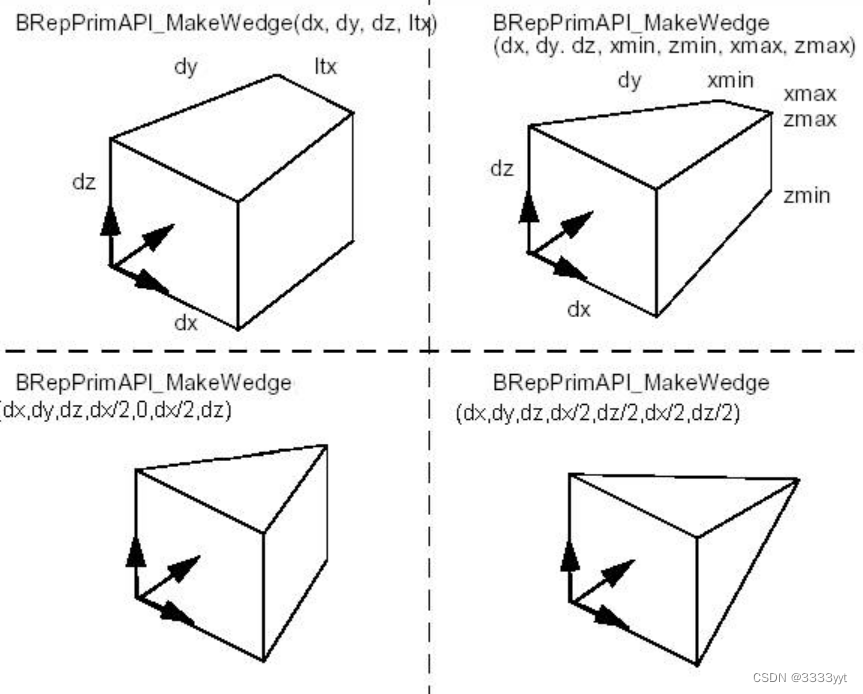
BRepPrimAPI_MakeWedge类允许构建一个楔形,这是一个倾斜的盒子,即一个有角度的盒子。楔形的构造方式与盒子的构造方式大致相同,即由三维dx,dy,dz加上参数,或由轴系,三维和参数构成。
下图显示了构建楔形的两种方法。一种是增加一个维度ltx,这是脸在x点的长度,第二种是增加xmin, xmax, zmin和zmax来描述面在dy点的长度。
第一个方法是第二个方法的特殊情况,其中xmin = 0, xmax = ltx, zmin = 0, zmax = dz。要制作居中金字塔,可以使用xmin = xmax = dx / 2, zmin = zmax = dz / 2。
旋转体
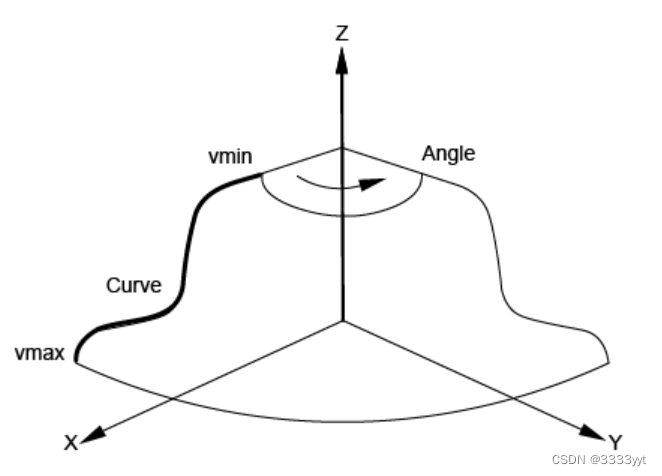
BRepPrimAPI_MakeOneAxis是一个延迟的类,用于所有构造旋转的基础对象的类的根类。旋转基元是通过绕轴旋转曲线来创建的。它们包括圆柱、圆锥、球面、环面和提供所有其他曲线的旋转。
描述了这些基础对象的特定结构,但它们都有一些共同的参数,它们是:
OneAxis构造的结果是一个实体、一个壳或一个面。面是覆盖旋转表面的面。请记住,您不会直接使用OneAxis,而是使用一个派生类,它提供了改进的结构。下图展示了OneAxis参数。
柱体
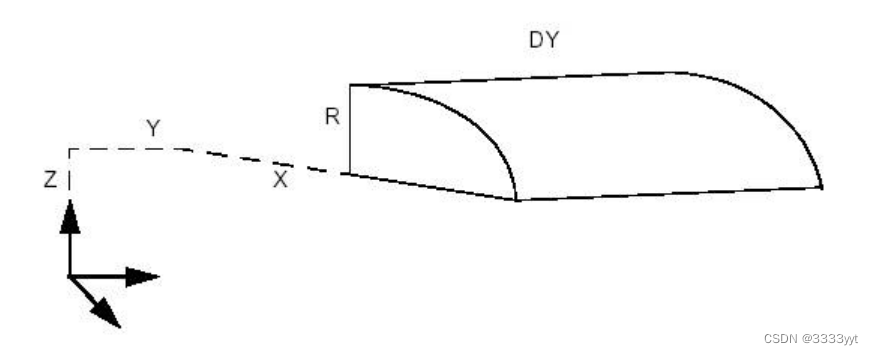
Breprimapi_MakeCylder类允许创建圆柱形基础对象。圆柱体可以在默认坐标系中创建,也可以在给定坐标系gp_Ax2中创建。有两种结构:
下面的代码构建图形的圆柱面,它是沿Y轴的圆柱面的四分之一,原点为X,Y,Z,长度为DY,半径为R。
Standard_Real X = 20, Y = 10, Z = 15, R = 10, DY = 30;
// Make the system of coordinates
gp_Ax2 axes = gp::ZOX();
axes.Translate(gp_Vec(X,Y,Z));
TopoDS_Face F =
BRepPrimAPI_MakeCylinder(axes,R,DY,PI/2.);
圆台
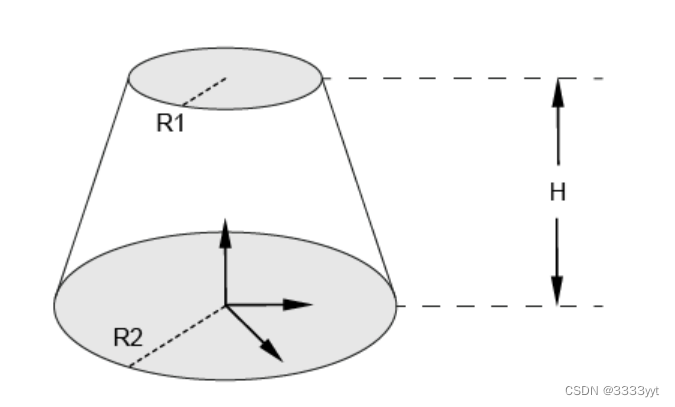
BRepPrimAPI_MakeCone类允许创建圆锥形基础对象。与圆柱体一样,锥体可以在默认坐标系中创建,也可以在给定坐标系(gp_Ax2)中创建。有两种结构:
下面的代码构建图形的实心锥体,它位于默认系统中,半径为R1和R2,高度为H。
Standard_Real R1 = 30, R2 = 10, H = 15;
TopoDS_Solid S = BRepPrimAPI_MakeCone(R1,R2,H);
球
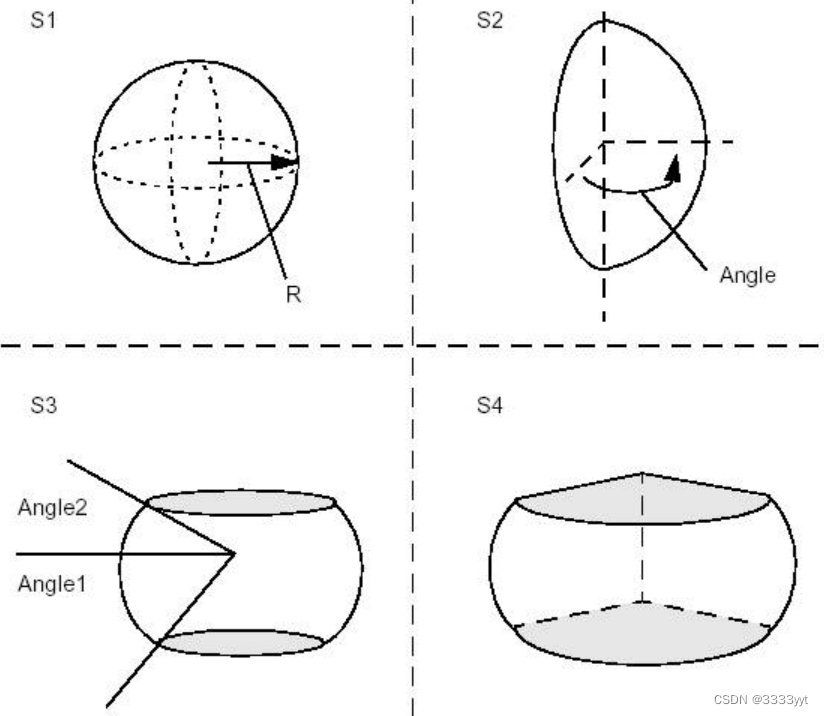
BRepPrimAPI_MakeSphere类允许创建球形原语。与圆柱体一样,球体可以在默认坐标系中创建,也可以在给定坐标系gp_Ax2中创建。有四种结构:
下面的代码从一个半径和三个角度构建了四个球体。
Standard_Real R = 30, ang = PI/2, a1 = -PI/2.3, a2 = PI/4;
TopoDS_Solid S1 = BRepPrimAPI_MakeSphere(R);
TopoDS_Solid S2 = BRepPrimAPI_MakeSphere(R,ang);
TopoDS_Solid S3 = BRepPrimAPI_MakeSphere(R,a1,a2);
TopoDS_Solid S4 = BRepPrimAPI_MakeSphere(R,a1,a2,ang);
注意,我们同样可以选择创建shell而不是solid。
圆环面
Breprrimapi_MakeTorus类允许创建环面基元。与其他基元一样,环面是在默认坐标系或给定坐标系gp_Ax2中创建的。与球体结构类似的结构有四种:
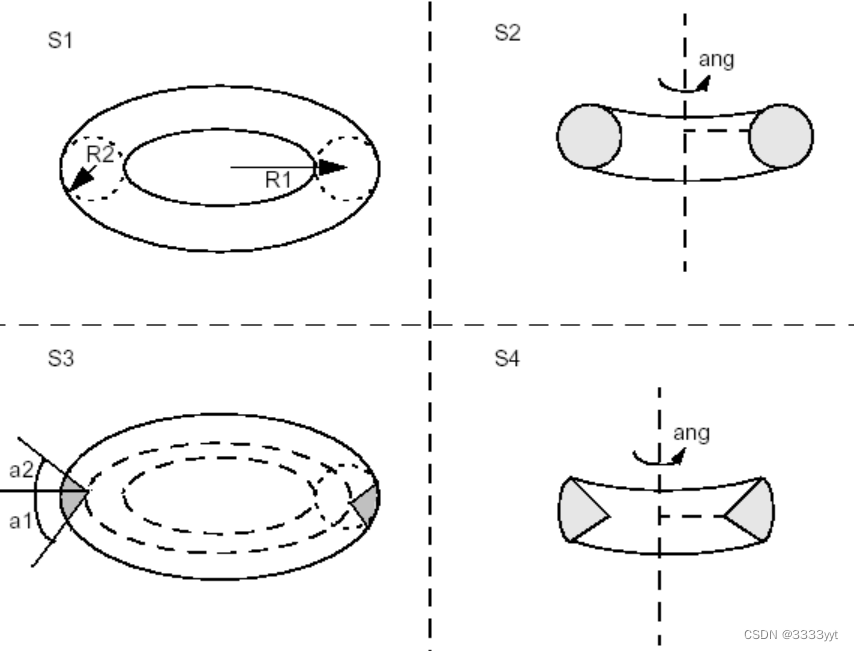
下面的代码从两个半径和三个角度构建四个环面壳。
Standard_Real R1 = 30, R2 = 10, ang = PI, a1 = 0, a2 = PI/2;
TopoDS_Shell S1 = BRepPrimAPI_MakeTorus(R1,R2);
TopoDS_Shell S2 = BRepPrimAPI_MakeTorus(R1,R2,ang);
TopoDS_Shell S3 = BRepPrimAPI_MakeTorus(R1,R2,a1,a2);
TopoDS_Shell S4 = BRepPrimAPI_MakeTorus(R1,R2,a1,a2,ang);
注意,我们同样可以选择创建实体而不是壳。
旋转
Breprrimapi_MakeRevolution类允许从曲线构建单轴原语。与其他单轴原语一样,它可以在默认坐标系或给定坐标系中创建。
曲线可以是任意的Geom_Curve,只要它是平面的,并且与本地坐标系的z轴在同一平面上。有四种结构模式:
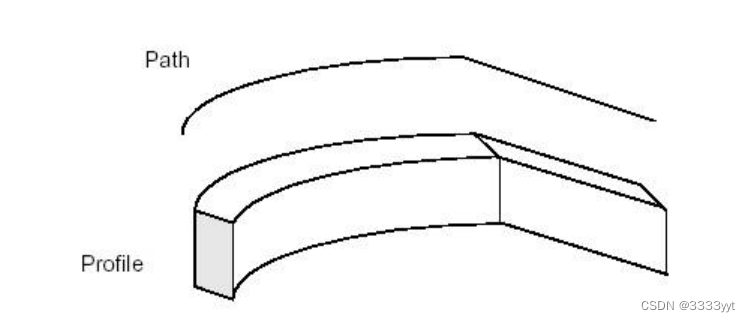
扫掠:棱镜,旋转和管道
扫掠
扫描是通过沿着路径扫描轮廓获得的对象。该轮廓可以是任何拓扑结构。路径通常是一条曲线或一条线。轮廓根据以下规则生成对象:
禁止扫略实体和复合实体。一个复合对象生成一个复合对象,并扫描它的所有元素。
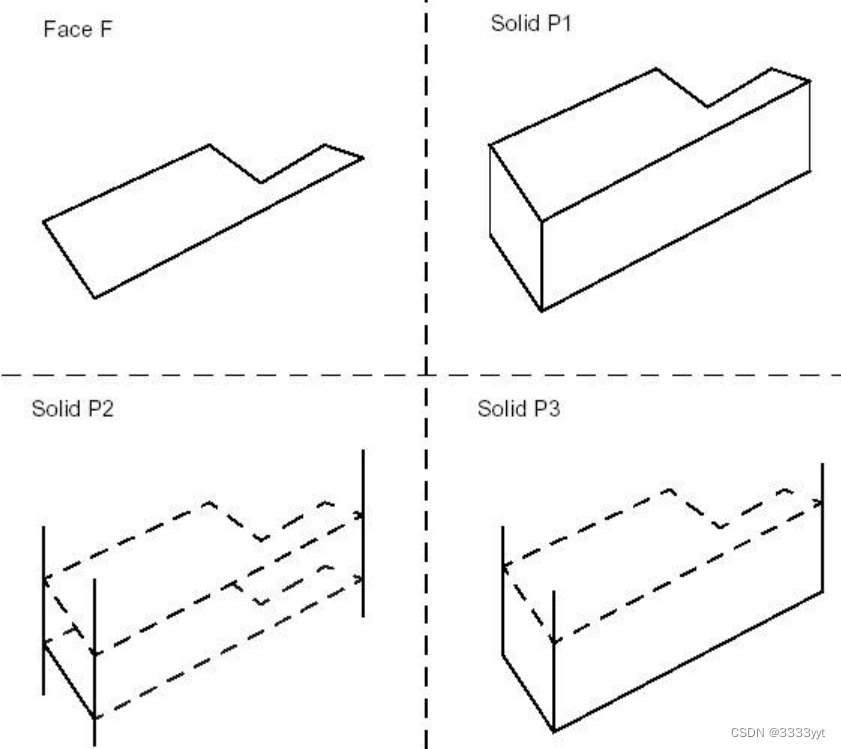
棱镜
BRepPrimAPI_MakeSweep类是一个延迟的类,用作以下扫描类的根:
BRepPrimAPI_MakePrism类允许从形状和矢量或方向创建线性棱镜。
下面的代码使用面、方向和长度创建有限、无限和半无限的实体。
TopoDS_Face F = ..; // The swept face
gp_Dir direc(0,0,1);
Standard_Real l = 10;
// create a vector from the direction and the length
gp_Vec v = direc;
v *= l;
TopoDS_Solid P1 = BRepPrimAPI_MakePrism(F,v);
// finite
TopoDS_Solid P2 = BRepPrimAPI_MakePrism(F,direc);
// infinite
TopoDS_Solid P3 = BRepPrimAPI_MakePrism(F,direc,Standard_False);
// semi-infinite
旋转
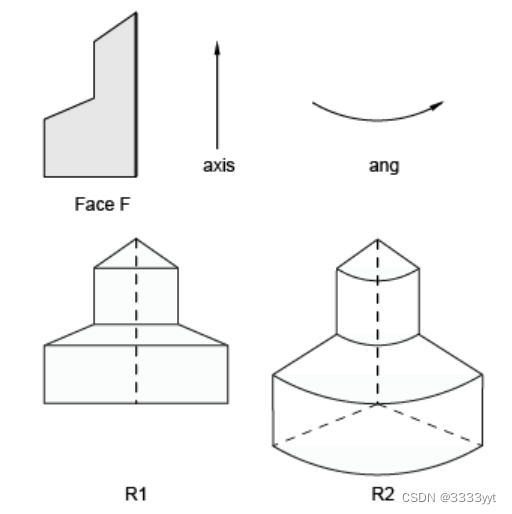
BRepPrimAPI_MakeRevol类允许从形状、轴(gp_Ax1)和角度创建旋转扫描。这个角度的默认值是2*PI,这意味着一个封闭的公转。
Breprrimapi_MakeRevol构造函数有最后一个参数来复制或共享原始形状。下面的代码使用一个面、一个轴和一个角度创建一个完全旋转和一个部分旋转。
TopoDS_Face F = ...; // the profile
gp_Ax1 axis(gp_Pnt(0,0,0),gp_Dir(0,0,1));
Standard_Real ang = PI/3;
TopoDS_Solid R1 = BRepPrimAPI_MakeRevol(F,axis);
// Full revol
TopoDS_Solid R2 = BRepPrimAPI_MakeRevol(F,axis,ang);
布尔运算
布尔运算用于从两组形状的组合中创建新形状。
从拓扑学的角度来看,这些是拓扑操作之后的混合(将圆角放在拓扑操作后创建的边缘上)。
拓扑操作是创建真实工业部件最方便的方法。由于大多数工业零件由几个简单的元素组成,如齿轮,臂,孔,肋,管和管道。通常很容易分别创建这些元素,然后在整个最后部分通过布尔运算将它们组合起来。
输入和结果参数
布尔运算具有以下类型的参数,并产生以下结果:
执行
BRepAlgoAPI_BooleanOperation类是布尔操作的延迟根类。
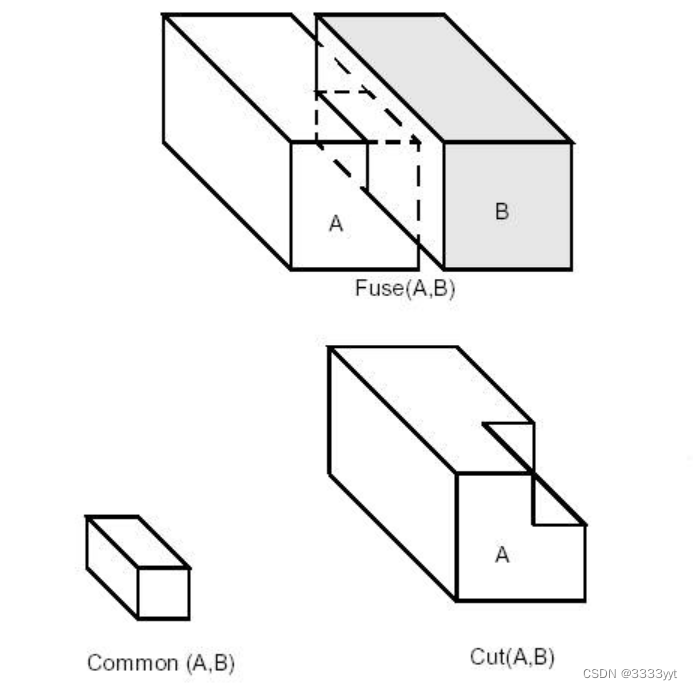
Fuse
BRepAlgoAPI_Fuse执行Fuse操作。
TopoDS_Shape A = ..., B = ...;
TopoDS_Shape S = BRepAlgoAPI_Fuse(A,B);
Common
BRepAlgoAPI_Common执行普通操作。
TopoDS_Shape A = ..., B = ...;
TopoDS_Shape S = BRepAlgoAPI_Common(A,B);
Cut
BRepAlgoAPI_Cut执行Cut操作。
TopoDS_Shape A = ..., B = ...;
TopoDS_Shape S = BRepAlgoAPI_Cut(A,B);
Section
BRepAlgoAPI_Section执行该section,描述为由TopoDS_Edge组成的TopoDS_Compound。
TopoDS_Shape A = ..., TopoDS_ShapeB = ...;
TopoDS_Shape S = BRepAlgoAPI_Section(A,B);
拓扑工具
OCCT提供算法:
从边缘创建线;
用线创造出面孔;
计算该形状相对于其他形状的状态;
在容器中定位形状;
从现有的形状中创建新的形状;
在面上建立边缘的p曲线;
检查形状的有效性;
获取面上的点;
获取面上的法线方向。
从线框模型中创建面
可以从三维空间中随机设置的任意平面边集创建平面面。这个功能可能是有用的,如果你需要从线框模型中恢复形状:
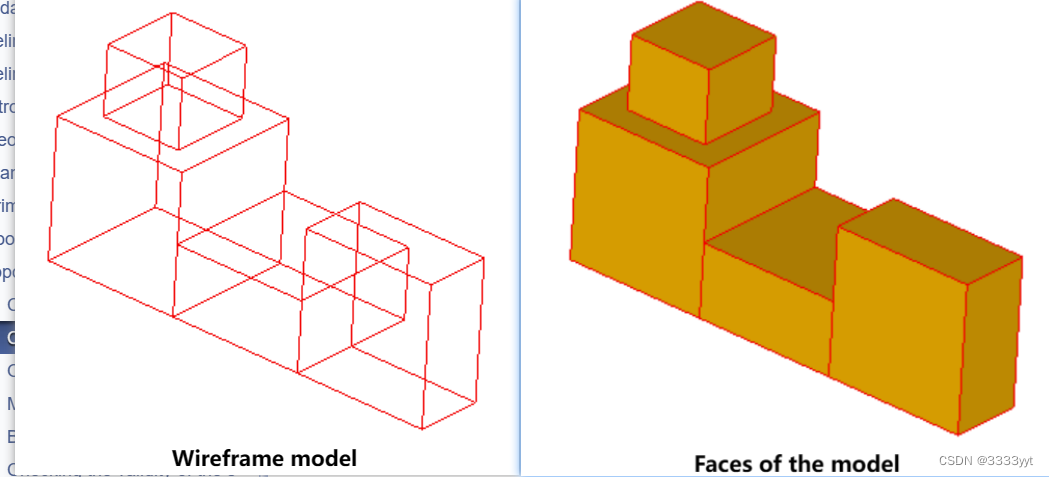
为了从边缘制作面,首先需要从给定的边缘创建平面线,然后从每条线创建平面面。静态方法BOPAlgo_Tools::EdgesToWires和BOPAlgo_Tools::WiresToFaces可以用于此:
TopoDS_Shape anEdges = ...; /* The input edges */
Standard_Real anAngTol = 1.e-8; /* The angular tolerance for distinguishing the planes in which the wires are located */
Standard_Boolean bShared = Standard_False; /* Defines whether the edges are shared or not */
//
TopoDS_Shape aWires; /* resulting wires */
Standard_Integer iErr = BOPAlgo_Tools::EdgesToWires(anEdges, aWires, bShared, anAngTol);
if (iErr) {cout << "Error: Unable to build wires from given edgesn";return;
}
//
TopoDS_Shape aFaces; /* resulting faces */
Standard_Boolean bDone = BOPAlgo_Tools::WiresToFaces(aWires, aFaces, anAngTol);
if (!bDone) {cout << "Error: Unable to build faces from wiresn";return;
}
这些方法也可以单独使用:
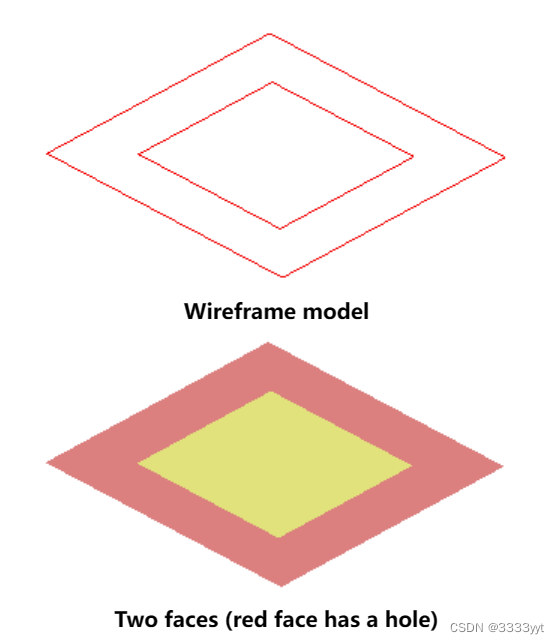
形状的分类
以下方法可以将不同形状相对于其他形状进行分类:
容器中形状的方向
以下方法允许重新定向容器中的形状:
创建新形状
以下方法允许从现有形状创建新形状:
创建P曲线
下面的方法允许在面上建立边缘的p曲线:
BOPTools_AlgoTools::BuildPCurveForEdgeOnFace计算面部边缘的PCurve;
检查形状的有效性
以下方法允许检查形状的有效性:
获取面上的点
以下方法可以在面部内部取点:
获取面上的法线
以下方法允许获得面/表面的法线方向:
Topology API
开放级联技术(OCCT)的拓扑API包括以下六个包:
API提供的类具有以下特性:
让我们使用类BRepBuilderAPI_MakeEdge从两点创建一条线性边。
gp_Pnt P1(10,0,0), P2(20,0,0);
TopoDS_Edge E = BRepBuilderAPI_MakeEdge(P1,P2);
这是从两点P1和P2创建边E的最简单方法,但开发人员可以在对数据不像前一个示例那样有信心时测试错误。
#include
#include
#include
void EdgeTest()
{
gp_Pnt P1;
gp_Pnt P2;
BRepBuilderAPI_MakeEdge ME(P1,P2);
if (!ME.IsDone())
{
// doing ME.Edge() or E = ME here
// would raise StdFail_NotDone
Standard_DomainError::Raise
(“ProcessPoints::Failed to createan edge”);
}
TopoDS_Edge E = ME;
}
在这个例子中,引入了一个中间对象ME。可以在访问结果之前测试函数是否完成。关于拓扑编程接口中的错误处理的更多信息可以在下一节中找到。
BRepBuilderAPI_MakeEdge提供了有价值的信息。例如,当从两个点创建一条边时,必须从这些点创建两个顶点。有时,您可能对快速获得这些顶点而不探索新边感兴趣。这样的信息可以在使用类时提供。下面的例子展示了一个从两个点创建一条边和两个顶点的函数。
void MakeEdgeAndVertices(const gp_Pnt& P1,
const gp_Pnt& P2,
TopoDS_Edge& E,
TopoDS_Vertex& V1,
TopoDS_Vertex& V2)
{
BRepBuilderAPI_MakeEdge ME(P1,P2);
if (!ME.IsDone()) {
Standard_DomainError::Raise
(“MakeEdgeAndVerices::Failed to create an edge”);
}
E = ME;
V1 = ME.Vextex1();
V2 = ME.Vertex2();
类BRepBuilderAPI_MakeEdge提供了两个方法Vertex1和Vertex2,它们返回用于创建边缘的两个顶点。
BRepBuilderAPI_MakeEdge如何既是一个函数又是一个类?它可以做到这一点,因为它使用了c++的强制转换功能。BRepBuilderAPI_MakeEdge类有一个叫做Edge的方法;在前面的示例中,可以这样写E = ME行。
E = ME.Edge();
该指令告诉c++编译器,使用Edge方法将BRepBuilderAPI_MakeEdge隐式转换为TopoDS_Edge。这意味着当在需要TopoDS_Edge的地方找到BRepBuilderAPI_MakeEdge时,会自动调用此方法。
这个特性允许您提供类,这些类在需要时具有函数调用的简单性,在需要高级处理时具有类的强大功能。在描述拓扑编程接口类时解释了这种方法的所有优点。
历史记录支持
所有拓扑API算法都支持其参数的形状修改历史(或仅仅是历史)。通常,历史记录可用于以下类型的输入形状的子形状:
有些算法还支持solid的历史记录。
历史信息包括以下信息:
History是根据操作结果填充的。历史记录不能返回结果中不包含的任何形状。如果操作的结果是空形状,则所有输入形状都将被认为是已删除的,并且没有任何形状具有已修改和已生成的形状。
历史信息可以通过API方法访问:
删除形状
在操作过程中,如果满足以下所有条件,则认为该形状已删除:
例如,在两个相交实体之间的CUT操作中,位于工具实体内部的所有顶点/边/面将在操作期间被删除。
修改形状
如果结果形状包含形状的分割,而不是形状本身,则该形状在操作期间被认为是已修改的。该形状只能修改为具有相同尺寸的形状。结果形状中包含的形状的分割是从该形状修改的。修改后的形状是从输入形状的子形状创建的,并且通常重复其几何形状。
Modified元素列表将只包含对操作结果有贡献的元素。如果列表为空,则表示该形状未被修改,需要检查它是否已被删除。
例如,形状在任何方向上翻译后,其所有子形状将被修改为其翻译副本。
生成形状
如果结果形状中包含的形状是在操作期间生成的,并且与创建它们的形状具有不同的维度,则认为它们是从输入形状生成的。
生成的元素列表将只包含那些包含在操作结果中的元素。如果列表为空,则表示没有从该形状生成新的形状。
例如,在某个方向上挤压边缘将创建一个面。这个面将从边缘生成。
BRepTools_History
BRepTools_History是通用的历史工具,用于统一不同算法的历史。
BRepTools_History可以从任何支持标准历史方法的算法中创建*(IsDeleted(), Modified()*和Generated()):
// The arguments of the operation
TopoDS_Shape aS = ...;// Perform transformation on the shape
gp_Trsf aTrsf;
aTrsf.SetTranslationPart(gp_Vec(0, 0, 1));
BRepBuilderAPI_Transform aTransformer(aS, aTrsf); // Transformation API algorithm
const TopoDS_Shape& aRes = aTransformer.Shape();// Create the translation history object
TopTools_ListOfShape anArguments;
anArguments.Append(aS);
BRepTools_History aHistory(anArguments, aTransformer);
BRepTools_History也允许合并历史。因此,如果你有两个或多个后续操作,你可以从这些操作的历史记录中获得一个最终的历史记录:
Handle(BRepTools_History) aHist1 = ...; // History of first operation
Handle(BRepTools_History) aHist2 = ...; // History of second operation
可以将第二个历史合并到第一个历史中:
aHist1->Merge(aHist2);或者创建新的历史记录,保持两个历史记录不变:
Handle(BRepTools_History) aResHistory = new BRepTools_History;
aResHistory->Merge(aHist1);
aResHistory->Merge(aHist2);
合并历史和从API算法创建历史的可能性允许为新算法提供简单的历史支持。
绘制历史记录
DRAW History对算法的支持由三个基本命令提供:
有关绘制历史记录机制的更多信息,请参阅绘制用户指南-历史记录命令中的相应章节。
倒角和切削
这个库提供了在形状边缘上制作圆角和倒角的算法。处理以下情况:
如果存在凹面,则需要扩展的表面和不需要扩展的表面都进行处理。
形状倒角
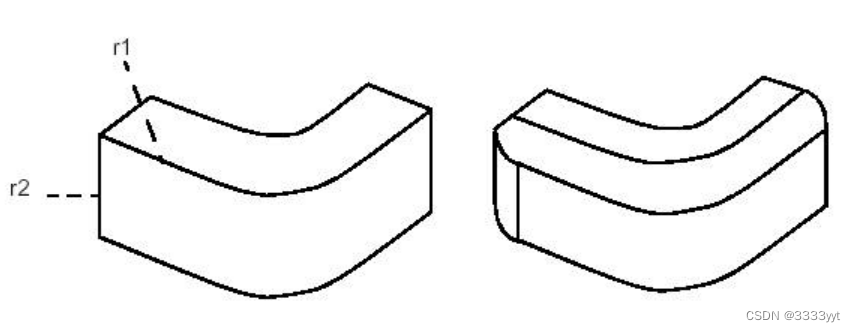
圆角是用光滑的表面代替锋利的边缘。
BRepFilletAPI_MakeFillet类允许对形状进行切片。
要生成圆角,必须在类的构造中定义圆角形状,并使用add方法添加圆角描述。
圆角描述包含一条边和一条半径。这条边必须由两个面共用。圆角自动扩展到与原始边缘平滑连续的所有边缘。添加两次圆角不是错误,最后一个描述成立。
在下面的示例中,创建一个尺寸为a,b,c,半径为r的圆角盒。
常半径
#include
#include
#include
#include
#include
#include TopoDS_Shape FilletedBox(const Standard_Real a, const Standard_Real b, const Standard_Real c, const Standard_Real r)
{ TopoDS_Solid Box = BRepPrimAPI_MakeBox(a,b,c); BRepFilletAPI_MakeFillet MF(Box); // add all the edges to fillet TopExp_Explorer ex(Box,TopAbs_EDGE); while (ex.More()) { MF.Add(r,TopoDS::Edge(ex.Current())); ex.Next(); } return MF.Shape(); } 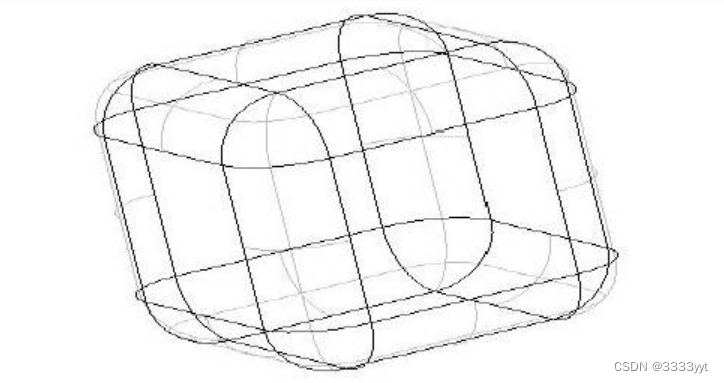
改变半径
#include
#include
#include
#include
#include
#include TopoDS_Shape FilletedBox(const Standard_Real a, const Standard_Real b, const Standard_Real c, const Standard_Real r)
{ TopoDS_Solid Box = BRepPrimAPI_MakeBox(a,b,c); BRepFilletAPI_MakeFillet MF(Box); // add all the edges to fillet TopExp_Explorer ex(Box,TopAbs_EDGE); while (ex.More()) { MF.Add(r,TopoDS::Edge(ex.Current())); ex.Next(); } return MF.Shape(); }
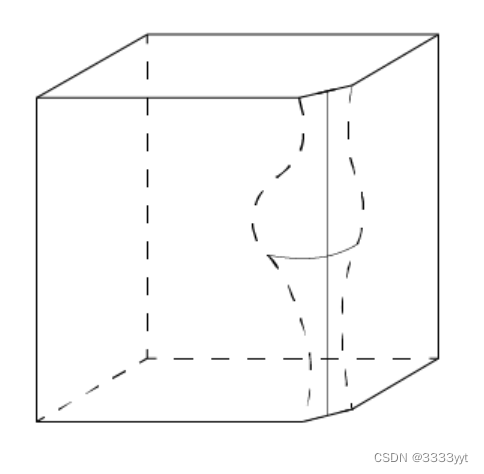
切削
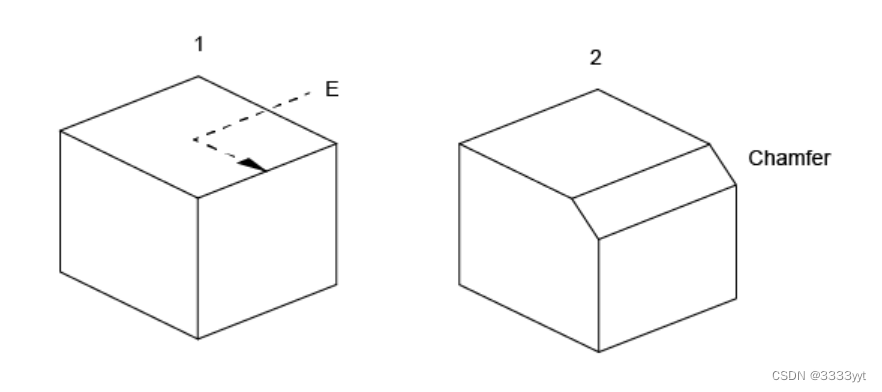
倒角是代替面的尖顶点的直线边缘。
BRepFilletAPI_MakeChamfer类的使用类似于BRepFilletAPI_MakeFillet类的使用,除了以下不同:
Add(dist, E, F)
Add(d1, d2, E, F) with d1 on the face F.
平面倒角
BRepFilletAPI_MakeFillet2d类允许在平面上构造圆角和倒角。在平面上创建圆角:定义圆角,指定要删除的顶点,并使用AddFillet方法给出圆角半径。
可以使用AddChamfer方法计算倒角。它可以用
如果面F2是由2D圆角和倒角生成器从面F1创建的,则生成器可以重建(生成器恢复其删除之前的状态)
BRepFilletAPI_MakeFillet2d builder;
builder.Init(F1,F2);
面倒角
#include “BRepPrimAPI_MakeBox.hxx”
#include “TopoDS_Shape.hxx”
#include “TopExp_Explorer.hxx”
#include “BRepFilletAPI_MakeFillet2d.hxx”
#include “TopoDS.hxx”
#include “TopoDS_Solid.hxx” TopoDS_Shape FilletFace(const Standard_Real a, const Standard_Real b, const Standard_Real c, const Standard_Real r) { TopoDS_Solid Box = BRepPrimAPI_MakeBox (a,b,c); TopExp_Explorer ex1(Box,TopAbs_FACE); const TopoDS_Face& F = TopoDS::Face(ex1.Current()); BRepFilletAPI_MakeFillet2d MF(F); TopExp_Explorer ex2(F, TopAbs_VERTEX); while (ex2.More()) { MF.AddFillet(TopoDS::Vertex(ex2.Current()),r); ex2.Next(); } // while... return MF.Shape();
}
Offsets, Drafts, Pipes and Evolved形状
这些类提供以下服务:
偏移计算
偏移量计算可以使用BRepOffsetAPI_MakeOffsetShape来执行。这个类为两种不同的偏移算法提供API:
基于解析延拓计算的偏移算法。参数含义请参见BRepOffsetAPI_MakeOffsetShape::PerformByJoin方法描述。下面的列表展示了该算法的主要方案:
第二种算法是,即没有连续的单个面总是可以建立偏移计算。下面的列表显示了简单的偏移算法:
下面的代码片段展示了用法示例:
BRepOffsetAPI_MakeOffsetShape OffsetMaker1;
// Computes offset shape using analytical continuation mechanism.
OffsetMaker1.PerformByJoin(Shape, OffsetValue, Tolerance);
if (OffsetMaker1.IsDone())NewShape = OffsetMaker1.Shape();BRepOffsetAPI_MakeOffsetShape OffsetMaker2;
// Computes offset shape using simple algorithm.
OffsetMaker2.PerformBySimple(Shape, OffsetValue);
if (OffsetMaker2.IsDone())NewShape = OffsetMaker2.Shape();
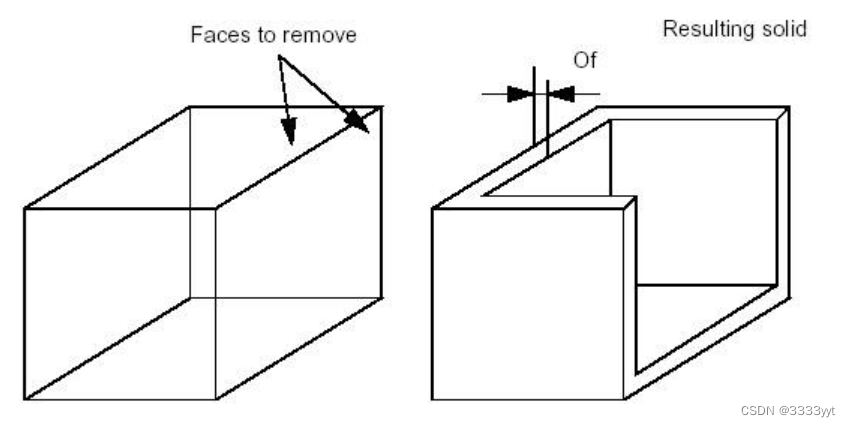
抽壳
抽壳用于将实体的给定面偏移一个特定的值。根据边缘的凹凸度,它沿其边缘使相邻的面圆或相交。BRepOffsetAPI_MakeThickSolid的MakeThickSolidByJoin方法接受实体、要删除的面列表和偏移量值作为输入。
TopoDS_Solid SolidInitial = ...;Standard_Real Of = ...;
TopTools_ListOfShape LCF;
TopoDS_Shape Result;
Standard_Real Tol = Precision::Confusion();for (Standard_Integer i = 1 ;i <= n; i++) {TopoDS_Face SF = ...; // a face from SolidInitialLCF.Append(SF);
}BRepOffsetAPI_MakeThickSolid SolidMaker;
SolidMaker.MakeThickSolidByJoin(SolidInitial,LCF,Of,Tol);
if (SolidMaker.IsDone())Result = SolidMaker.Shape();
也可以创建实体之间的壳,偏移壳。这个功能可以使用BRepOffsetAPI_MakeThickSolid::MakeThickSolidBySimple方法调用。下面的代码显示了使用示例:
BRepOffsetAPI_MakeThickSolid SolidMaker;
SolidMaker.MakeThickSolidBySimple(Shell, OffsetValue);
if (myDone.IsDone())Solid = SolidMaker.Shape();
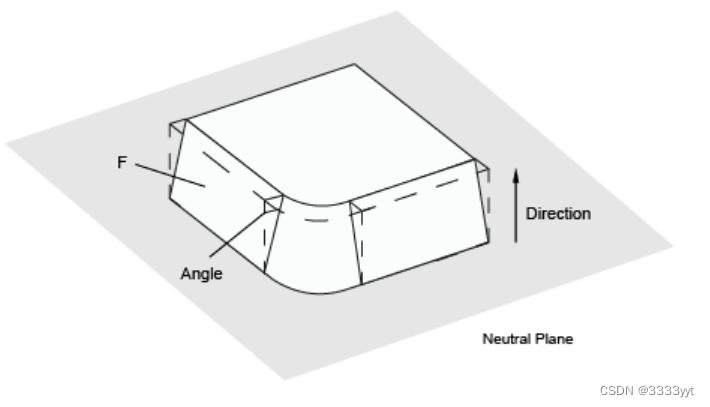
拔模角度
BRepOffsetAPI_DraftAngle类允许通过对其平面,圆柱形和圆锥形面应用拔模角度来修改形状。
类是从一个形状创建或初始化的,然后添加要修改的面;对于每个face,使用三个参数:
下面的代码在一个形状的几个面上放置一个拔模角;每个面使用相同的方向、角度和中性面:
TopoDS_Shape myShape = ...
// The original shape
TopTools_ListOfShape ListOfFace;
// Creation of the list of faces to be modified
... gp_Dir Direc(0.,0.,1.);
// Z direction
Standard_Real Angle = 5.*PI/180.;
// 5 degree angle
gp_Pln Neutral(gp_Pnt(0.,0.,5.), Direc);
// Neutral plane Z=5
BRepOffsetAPI_DraftAngle theDraft(myShape);
TopTools_ListIteratorOfListOfShape itl;
for (itl.Initialize(ListOfFace); itl.More(); itl.Next()) { theDraft.Add(TopoDS::Face(itl.Value()),Direc,Angle,Neutral); if (!theDraft.AddDone()) { // An error has occurred. The faulty face is given by // ProblematicShape break; }
}
if (!theDraft.AddDone()) { // An error has occurred TopoDS_Face guilty = theDraft.ProblematicShape(); ...
}
theDraft.Build();
if (!theDraft.IsDone()) { // Problem encountered during reconstruction ...
}
else { TopoDS_Shape myResult = theDraft.Shape(); ...
}
管状构建
BRepOffsetAPI_MakePipe类允许从Spine(一个Wire)和Profile(一个Shape)创建管道。此实现仅限于具有平滑过渡的脊线,锐利过渡由BRepOffsetAPI_MakePipeShell处理。更精确地说,连续性必须是G1,这意味着切线在相邻的边缘上必须有相同的方向,尽管不一定是相同的大小。
脊柱和轮廓之间的角度在整个管道中保持不变。
TopoDS_Wire Spine = ...;
TopoDS_Shape Profile = ...;
TopoDS_Shape Pipe = BRepOffsetAPI_MakePipe(Spine,Profile);
旋转实体
BRepOffsetAPI_MakeEvolved类允许从Spine(平面面或线)和profile(线)创建一个进化的实体。
进化的实体是由脊柱和轮廓产生的无环扫描。
通过在脊柱上扫描轮廓的参考轴来创建提升的实体。坐标轴的原点移动到脊柱,X轴和局部切线重合,Z轴垂直于面。
轮廓线的参考轴可以定义为以下两种不同的模式:
TopoDS_Face Spine = ...;
TopoDS_Wire Profile = ...;
TopoDS_Shape Evol =
BRepOffsetAPI_MakeEvolved(Spine,Profile);
对象修改
变换
BRepBuilderAPI_Transform类可用于对形状应用转换(参见类gp_Trsf)。这些方法有一个布尔参数,用于复制或共享原始形状,只要转换允许(只可能进行直接等距转换)。默认情况下,共享原始形状。
下面的示例处理形状的旋转。
TopoDS_Shape myShape1 = ...;
// The original shape 1
TopoDS_Shape myShape2 = ...;
// The original shape2
gp_Trsf T;
T.SetRotation(gp_Ax1(gp_Pnt(0.,0.,0.),gp_Vec(0.,0.,1.)),
2.*PI/5.);
BRepBuilderAPI_Transformation theTrsf(T);
theTrsf.Perform(myShape1);
TopoDS_Shape myNewShape1 = theTrsf.Shape()
theTrsf.Perform(myShape2,Standard_True);
// Here duplication is forced
TopoDS_Shape myNewShape2 = theTrsf.Shape()
复制
使用BRepBuilderAPI_Copy类复制一个形状。这样就形成了一个新的形状。下面以复制实体为例:
TopoDS Solid MySolid;
....// Creates a solid TopoDS_Solid myCopy = BRepBuilderAPI_Copy(mySolid);
TopologyAPI的错误句柄
方法可以在以下两种情况下报告错误:
第二种情况应该随着系统的调试和异常机制的处理而变得越来越异常。使用异常可以避免在调用方法时处理错误状态:这是一种非常繁琐的编程风格。
在第一种情况下,还应该引发异常,因为调用方法应该已经验证了参数,如果它没有这样做,则存在错误。例如,如果在调用MakeEdge之前,您不确定两点是否相同,则必须对这种情况进行测试。
对参数进行这些有效性检查对于编程来说可能是乏味的,并且令人沮丧,因为您可能已经正确地推测该方法将执行两次测试。它不信任你。由于该测试涉及大量计算,因此执行两次也很耗时。
因此,您可能会倾向于采用以下示例中所示的极不可取的编程风格:
#include
try {
TopoDS_Edge E = BRepBuilderAPI_MakeEdge(P1,P2);
// go on with the edge
}
catch {
// process the error.
}
为了帮助用户,Topology API类只引发异常StdFail_NotDone。任何其他异常都意味着在这个API的设计中发生了无法预料的事情。
只有当用户试图访问计算结果并且原始数据已损坏时,才会引发NotDone异常。在构造类实例时,如果不能完成算法,则设置内部标志NotDone。可以测试此标志,并且在某些情况下可以查询更完整的错误描述。如果用户忽略NotDone状态并尝试访问结果,则会引发异常。
BRepBuilderAPI_MakeEdge ME(P1,P2);
if (!ME.IsDone()) {
// doing ME.Edge() or E = ME here
// would raise StdFail_NotDone
Standard_DomainError::Raise
(“ProcessPoints::Failed to create an edge”);
}
TopoDS_Edge E = ME;
缝合
介绍
缝纫允许从一组独立的拓扑元素(面和边)创建连接的拓扑(壳和线)。例如,缝纫可以用来从一个单独的面复合创建一个壳。
区分缝合和其他修改几何形状的程序是很重要的,例如填充孔或间隙、粘合、弯曲曲线和表面等。
缝合不会改变形状的几何表示。缝合适用于没有连接但可以连接的拓扑元素(面,边),因为它们在几何上是一致的:它增加了拓扑连通性的信息。已经连接的元件在流形缝合的情况下保持不变。
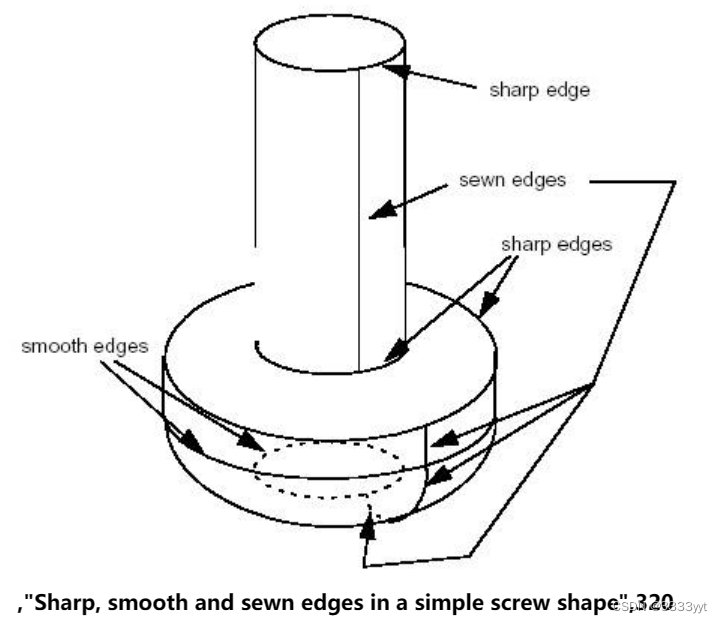
让我们定义几个术语:
缝合算法
缝制算法是形状加工的基本算法之一,缝制算法的质量非常重要。
缝纫算法在类BRepBuilder_Sewing中实现。这个类提供了以下方法:
缝合支持大值公差的工作方式。不需要一步一步地重复缝合,同时平稳地增加公差。
也可以将边缘缝到金属丝上,也可以将局部分离的面和边缘缝到形状上。
缝合算法可以细分为几个独立的阶段,其中一些可以使用布尔或其他标志打开或关闭。
简而言之,该算法需要为每个自由边界找到一组合并候选者,并根据一定的标准对其进行筛选,最后将发现的候选者合并并构建最终的缝合形状。
算法的每个阶段或整个算法都可以通过以下参数进行调整:
示例
要连接一组n个连续但独立的面,请执行以下操作:
BRepBuilderAPI_Sewing Sew;
Sew.Add(Face1);
Sew.Add(Face2);
...
Sew.Add(Facen);
Sew.Perform();
TopoDS_Shape result= Sew.SewedShape();
如果所有的面都缝对了,结果就是一个壳。否则,它就是一个复合对象。在一次成功的缝合操作后,所有的面都有一个一致的方向。
容差管理
为了生产一个封闭的外壳,缝纫允许指定工作公差值,超过属于形状的小面尺寸。
然而,如果我们生产一个开壳,如果工作公差值太大(即超过了位于开放边界上的面的尺寸),则可能会得到不正确的缝纫结果。
以下建议可用于调整缝纫过程:
流形和非流形
为了从一组面中创建一个或多个壳,缝纫将属于不同面或一个封闭面的边合并在一起。
面缝支持多种和非多种模式。流形模式只能产生一个流形外壳。缝纫应在非流形模式下使用,以创建非流形外壳。
面形缝只将属于不同面或一个封闭面的最近的两条边合并在一起。面的非流形缝将所有边以小于规定公差的距离合并。
对于复杂的拓扑结构,建议先应用歧管缝,然后应用非歧管缝,以尽可能减小工作公差。但是,对于简单的拓扑来说,这不是必需的。
给非流形缝合一个大的公差值将导致很多不正确,因为所有附近的几何形状将被缝合。
局部缝合
如果一个形状在缝制后仍有一些未缝制的面或边缘,则可以使用更大公差的局部缝制。
局部缝纫尤其适用于开壳。它允许在形状的一部分缝一个不需要的孔,并保持一个所需的孔,这比在形状的另一部分为局部缝制指定的工作公差小。局部缝制比整体缝制要快得多。
所有预先存在的整体形状的连接都在局部缝制后保留。
例如,如果你想用局部缝线缝合两个有重合自由边的开壳,有必要从两个壳中创建一个复合,然后使用方法BRepBuilderAPI_Sewing:: load()加载完整的复合。之后需要添加局部子形状,应该使用方法BRepBuilderAPI_Sewing:: add()来缝制。缝纫的结果可以使用方法BRepBuilderAPI_Sewing::SewedShape()获得。
看一个示例
//initial sewn shapes
TopoDS_Shape aS1, aS2; // these shapes are expected to be well sewn shells
TopoDS_Shape aComp;
BRep_Builder aB;
aB.MakeCompound(aComp);
aB.Add(aComp, aS1);
aB.Add(aComp, aS2);
................................
aSewing.Load(aComp);//sub shapes which should be locally sewed
aSewing.Add(aF1);
aSewing.Add(aF2);
//performing sewing
aSewing.Perform();
//result shape
TopoDS_Shape aRes = aSewing.SewedShape();
特征
BRepFeat包中包含的这个库对于创建和操作超越经典形状边界表示的形式和机械特征是必要的。从这个意义上说,BRepFeat是BRepBuilderAPI包的扩展。
形状特征
形状特征是凹陷或突出,包括以下类型:
根据你是想做一个凹陷还是突出,你可以选择移除物质(布尔剪切:熔合等于0)或添加物质(布尔融合:融合等于1)。
形状特征创建的语义基于形状的构造:
定义特征结构的形状既可以是支撑边,也可以是面部的相关区域。
在有支撑边的情况下,该轮廓可以通过绑定附着在基形的一个面上。当轮廓被绑定到该面上时,轮廓将在该面上滑动的信息将提供给相关的类方法。例如,对于面的相关区域,您可以将其切割出来并在不同的高度移动,这定义了突出或凹陷的限制面。
具有这种局部操作的拓扑定义使计算比全局操作更简单、更快。后者将需要第二阶段去除不需要的物质以获得相同的结果。
Form来自 BRepFeat包是一个延迟的类,用作表单特性的根。它继承了来自BRepBuilderAPI的MakeShape,并提供了跟踪所有子形状的方法的实现。
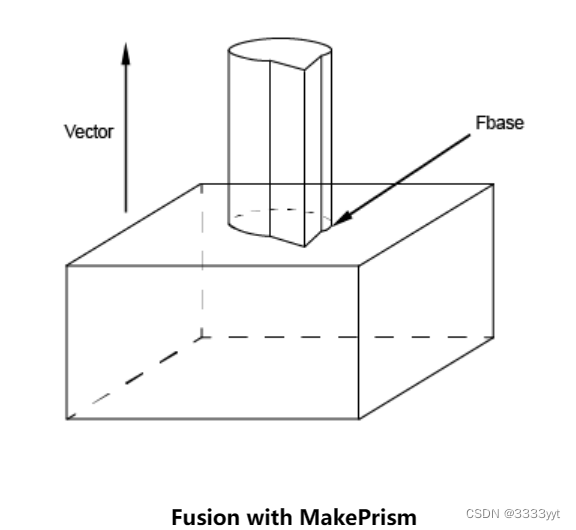
棱镜
类BRepFeat_MakePrism用于构建与形状交互的棱镜。它被创建或初始化
有六种Perform方法:
请注意,Add方法可以在Perform方法之前使用,以指示由边缘生成的面滑入基本形状的面。
在以下顺序中,执行突出,即将形状的一个面更改为棱镜。
TopoDS_Shape Sbase = ...; // an initial shape
TopoDS_Face Fbase = ....; // a base of prism gp_Dir Extrusion (.,.,.); // An empty face is given as the sketch face BRepFeat_MakePrism thePrism(Sbase, Fbase, TopoDS_Face(), Extrusion, Standard_True, Standard_True); thePrism, Perform(100.);
if (thePrism.IsDone()) { TopoDS_Shape theResult = thePrism; ...
}
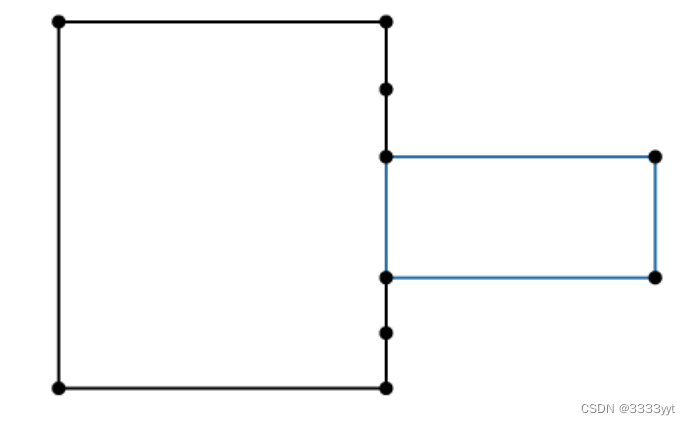
拔模棱镜
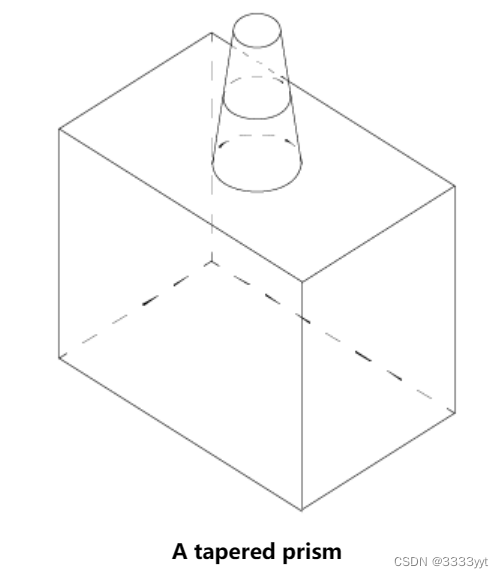
类BRepFeat_MakeDPrism用于构建与基本形状交互的草稿棱镜拓扑。这些可能是凹陷或突出。创建或初始化一个类对象:
显然,MakeDPrism的输入数据与MakePrism相同,除了增加了一个参数Angle和缺少了一个参数Direction:棱镜生成的方向是自动确定为棱镜基部的法线。拔模棱镜特征创建的语义是基于形状的构造:
所述拔模棱镜特征的形状定义结构可以是支撑边或面的有关区域。
在支撑边的情况下,该轮廓可以通过绑定附着在基形的一个面上。当轮廓被绑定到该面上时,轮廓将在该面上滑动的信息将提供给相关的类方法。对于面部的相关区域,可以将其切割出来并移动到不同的高度,这将定义一个突出或凹陷方向的限制面部。
Perform方法与MakePrism的方法相同。
TopoDS_Shape S = BRepPrimAPI_MakeBox(400.,250.,300.);
TopExp_Explorer Ex;
Ex.Init(S,TopAbs_FACE);
Ex.Next();
Ex.Next();
Ex.Next();
Ex.Next();
Ex.Next();
TopoDS_Face F = TopoDS::Face(Ex.Current());
Handle(Geom_Surface) surf = BRep_Tool::Surface(F);
gp_Circ2d
c(gp_Ax2d(gp_Pnt2d(200.,130.),gp_Dir2d(1.,0.)),50.);
BRepBuilderAPI_MakeWire MW;
Handle(Geom2d_Curve) aline = new Geom2d_Circle(c);
MW.Add(BRepBuilderAPI_MakeEdge(aline,surf,0.,PI));
MW.Add(BRepBuilderAPI_MakeEdge(aline,surf,PI,2.*PI));
BRepBuilderAPI_MakeFace MKF;
MKF.Init(surf,Standard_False);
MKF.Add(MW.Wire());
TopoDS_Face FP = MKF.Face();
BRepLib::BuildCurves3d(FP);
BRepFeat_MakeDPrism MKDP (S,FP,F,10*PI180,Standard_True, Standard_True);
MKDP.Perform(200);
TopoDS_Shape res1 = MKDP.Shape();
旋转
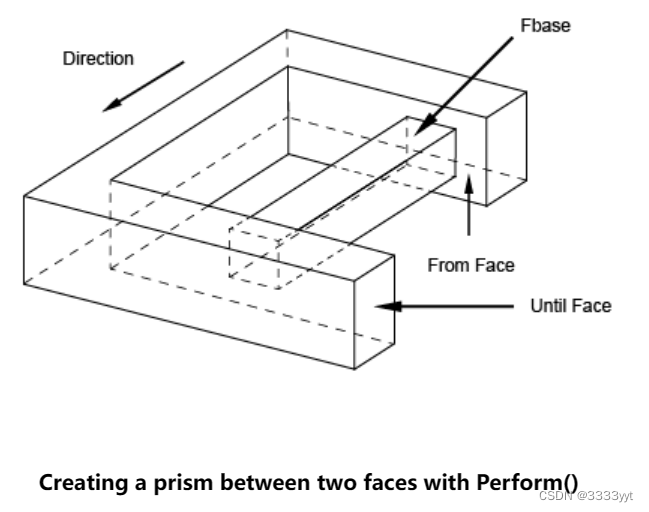
类BRepFeat_MakeRevol用于构建与形状交互的旋转。它被创建或初始化从:
有四种Perform方法:
请注意,Add方法可以在Perform方法之前使用,以指示由边缘生成的面滑入基本形状的面。
在下面的序列中,一个面被旋转,并且旋转被一个基本形状的面所限制。
TopoDS_Shape Sbase = ...; // an initial shape
TopoDS_Face Frevol = ....; // a base of prism
TopoDS_Face FUntil = ....; // face limiting the revol gp_Dir RevolDir (.,.,.);
gp_Ax1 RevolAx(gp_Pnt(.,.,.), RevolDir); // An empty face is given as the sketch face BRepFeat_MakeRevol theRevol(Sbase, Frevol, TopoDS_Face(), RevolAx, Standard_True, Standard_True); theRevol.Perform(FUntil);
if (theRevol.IsDone()) { TopoDS_Shape theResult = theRevol; ...
}
管道
类BRepFeat_MakePipe构造具有管道特征的复合形状:凹陷或突出。创建或初始化一个类对象:
有三种Perform方法:
让我们来看看这个例子:
TopoDS_Shape S = BRepPrimAPI_MakeBox(400.,250.,300.);
TopExp_Explorer Ex;
Ex.Init(S,TopAbs_FACE);
Ex.Next();
Ex.Next();
TopoDS_Face F1 = TopoDS::Face(Ex.Current());
Handle(Geom_Surface) surf = BRep_Tool::Surface(F1);
BRepBuilderAPI_MakeWire MW1;
gp_Pnt2d p1,p2;
p1 = gp_Pnt2d(100.,100.);
p2 = gp_Pnt2d(200.,100.);
Handle(Geom2d_Line) aline = GCE2d_MakeLine(p1,p2).Value(); MW1.Add(BRepBuilderAPI_MakeEdge(aline,surf,0.,p1.Distance(p2)));
p1 = p2;
p2 = gp_Pnt2d(150.,200.);
aline = GCE2d_MakeLine(p1,p2).Value(); MW1.Add(BRepBuilderAPI_MakeEdge(aline,surf,0.,p1.Distance(p2)));
p1 = p2;
p2 = gp_Pnt2d(100.,100.);
aline = GCE2d_MakeLine(p1,p2).Value(); MW1.Add(BRepBuilderAPI_MakeEdge(aline,surf,0.,p1.Distance(p2)));
BRepBuilderAPI_MakeFace MKF1;
MKF1.Init(surf,Standard_False);
MKF1.Add(MW1.Wire());
TopoDS_Face FP = MKF1.Face();
BRepLib::BuildCurves3d(FP);
TColgp_Array1OfPnt CurvePoles(1,3);
gp_Pnt pt = gp_Pnt(150.,0.,150.);
CurvePoles(1) = pt;
pt = gp_Pnt(200.,100.,150.);
CurvePoles(2) = pt;
pt = gp_Pnt(150.,200.,150.);
CurvePoles(3) = pt;
Handle(Geom_BezierCurve) curve = new Geom_BezierCurve
(CurvePoles);
TopoDS_Edge E = BRepBuilderAPI_MakeEdge(curve);
TopoDS_Wire W = BRepBuilderAPI_MakeWire(E);
BRepFeat_MakePipe MKPipe (S,FP,F1,W,Standard_False,
Standard_True);
MKPipe.Perform();
TopoDS_Shape res1 = MKPipe.Shape();

机械特征
机械特征包括沿平面(线性)表面或旋转表面的肋、突起和凹槽(或槽)、凹陷。
机械特征的语义是围绕给轮廓赋予厚度而建立的。这种厚度可以是对称的(在轮廓的一侧),也可以是不对称的(在两侧)。在形状特征的语义中,厚度是由特定上下文中的形状构造来定义的。
然而,在机械特性的情况下,开发背景有所不同。这里包括挤压:
创建或初始化一个类对象
线性形式
线性形式是在MakeLinearForm类中实现的,它沿着平面创建一个肋骨或凹槽。有一个Perform()方法,它沿着与基形Sbase交互的direction1和direction2从导线执行棱镜。棱镜的高度为Magnitude(Direction1)+Magnitude(direction2)。
BRepBuilderAPI_MakeWire mkw;
gp_Pnt p1 = gp_Pnt(0.,0.,0.);
gp_Pnt p2 = gp_Pnt(200.,0.,0.);
mkw.Add(BRepBuilderAPI_MakeEdge(p1,p2));
p1 = p2;
p2 = gp_Pnt(200.,0.,50.);
mkw.Add(BRepBuilderAPI_MakeEdge(p1,p2));
p1 = p2;
p2 = gp_Pnt(50.,0.,50.);
mkw.Add(BRepBuilderAPI_MakeEdge(p1,p2));
p1 = p2;
p2 = gp_Pnt(50.,0.,200.);
mkw.Add(BRepBuilderAPI_MakeEdge(p1,p2));
p1 = p2;
p2 = gp_Pnt(0.,0.,200.);
mkw.Add(BRepBuilderAPI_MakeEdge(p1,p2));
p1 = p2;
mkw.Add(BRepBuilderAPI_MakeEdge(p2,gp_Pnt(0.,0.,0.)));
TopoDS_Shape S = BRepBuilderAPI_MakePrism(BRepBuilderAPI_MakeFace (mkw.Wire()),gp_Vec(gp_Pnt(0.,0.,0.),gp_P nt(0.,100.,0.)));
TopoDS_Wire W = BRepBuilderAPI_MakeWire(BRepBuilderAPI_MakeEdge(gp_Pnt (50.,45.,100.),
gp_Pnt(100.,45.,50.)));
Handle(Geom_Plane) aplane = new Geom_Plane(gp_Pnt(0.,45.,0.), gp_Vec(0.,1.,0.));
BRepFeat_MakeLinearForm aform(S, W, aplane, gp_Dir (0.,5.,0.), gp_Dir(0.,-3.,0.), 1, Standard_True);
aform.Perform();
TopoDS_Shape res = aform.Shape();
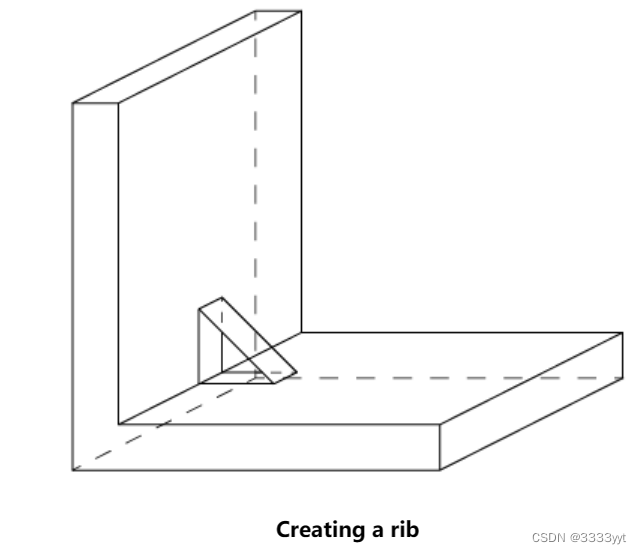
胶粘
类BRepFeat_Gluer允许沿面粘合两个实体。胶合成型的接触面不得在基本成型的接触面外有零件。完成后,该算法给出粘合形状,并在形状内切割出部分面。
类是从两个形状创建或初始化的:“粘合”形状和基本形状(另一个形状粘在其上)。使用两种绑定方法将粘合形状的面绑定到基本形状的面,将粘合形状的边缘绑定到基本形状的边缘。
注意,每个面和边都必须有界,如果两个粘合面的两个边是一致的,它们必须明确有界。
TopoDS_Shape Sbase = ...; // the basic shape
TopoDS_Shape Sglued = ...; // the glued shape TopTools_ListOfShape Lfbase;
TopTools_ListOfShape Lfglued;
// Determination of the glued faces
... BRepFeat_Gluer theGlue(Sglue, Sbase);
TopTools_ListIteratorOfListOfShape itlb(Lfbase);
TopTools_ListIteratorOfListOfShape itlg(Lfglued);
for (; itlb.More(); itlb.Next(), itlg(Next()) {
const TopoDS_Face& f1 = TopoDS::Face(itlg.Value());
const TopoDS_Face& f2 = TopoDS::Face(itlb.Value());
theGlue.Bind(f1,f2);
// for example, use the class FindEdges from LocOpe to
// determine coincident edges
LocOpe_FindEdge fined(f1,f2);
for (fined.InitIterator(); fined.More(); fined.Next()) {
theGlue.Bind(fined.EdgeFrom(),fined.EdgeTo());
}
}
theGlue.Build();
if (theGlue.IsDone() {
TopoDS_Shape theResult = theGlue;
...
}
分割形状
类BRepFeat_SplitShape用于将形状的面分割成线或边。包含新实体的形状被重建,共享未修改的实体。
类是从一个形状(基本形状)创建或初始化的。Add方法有三种:
注:添加的线和边必须定义面上的闭合线或位于两个现有边之间的线。现有的边不能相交。
TopoDS_Shape Sbase = ...; // basic shape
TopoDS_Face Fsplit = ...; // face of Sbase
TopoDS_Wire Wsplit = ...; // new wire contained in Fsplit
BRepFeat_SplitShape Spls(Sbase);
Spls.Add(Wsplit, Fsplit);
TopoDS_Shape theResult = Spls;
...
3D 模型 特征
OCCT特征化算法旨在从模型中去除不需要的部分或特征。这些零件可以是孔、突起、间隙、倒角、圆角等。
不执行特征检测,所有要删除的特征都应该由用户定义。在特征化过程中不修改输入形状,结果中构建新的形状。
在API级别上,特征算法是在BRepAlgoAPI_Defeaturing类中实现的。在输入时,算法接受要从中去除的形状和要从形状中去除的特征(一个或多个)。目前,输入形状应该是SOLID、COMPSOLID或COMPOUND of SOLIDs。要删除的特征是由形成它们的面孔集定义的。如何给出特征面并不重要:作为单独的面还是它们的集合。这些面应该属于初始形状,否则它们将被忽略。
实际的特征移除是由底层的BOPAlgo_RemoveFeatures算法执行的。在API级别,所有输入都被传递到工具中,并调用方法BOPAlgo_RemoveFeatures::Perform()。
在删除特征之前,所有要从形状中删除的面都被分类到连接的块中-每个块代表一个要删除的特征。特征一个接一个地从形状中移除,这允许删除所有可能的特征,即使它们的移除存在一些问题(例如,由于不正确的输入数据)。
被移除的特征被相邻的面的扩展填充。一般来说,从形状中去除单个特征的算法如下:
如果单个特征去除成功,则结果形状被新形状覆盖,否则结果不保留,并给出警告。无论哪种方式,该过程都将继续进行下一个功能。
defaturing算法有以下选项:
以及基类(BOPAlgo_Options)中可用的选项:
注意,这里不支持基类的其他选项,也不会产生任何影响。
历史记录支持允许根据Modified、IsDeleted和Generated跟踪输入形状的修改。默认情况下,收集历史记录,但是可以使用SetToFillHistory(false)方法禁用它。在底层,历史信息由历史工具BRepTools_History收集,该工具可以通过BOPAlgo_RemoveFeatures:: history()方法访问。
错误/警告报告系统允许获得在操作期间发生的错误/警告的扩展概述。一旦出现任何错误,算法就会停止工作。警告允许继续作业,并通知用户出错了。该算法返回以下错误/警告:
有关错误/警告报告系统的更多信息,请参见布尔操作用户指南中的错误和警告报告系统一章。
并行处理模式-允许在并行模式下运行算法,更快地获得结果。
该算法有一定的局限性:
请注意,为了成功地移除特征,与特征相邻的扩展面应完全覆盖特征,否则将无法重建实体。看看下面这个简单的形状:
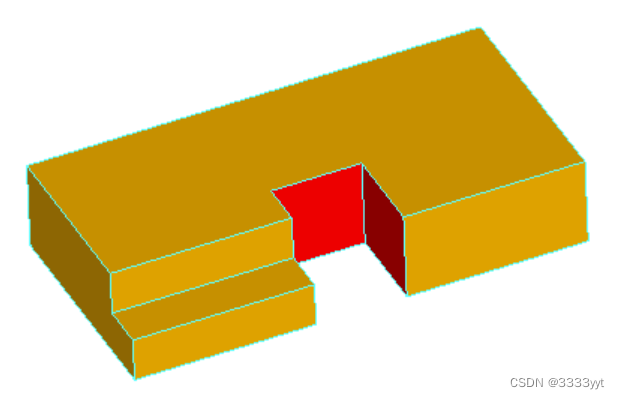
去除间隙的所有三个面是行不通的,因为没有面来填补横向部分的步骤。虽然,只去除两个面,保留一个横向面,将填补空白与保留的面:
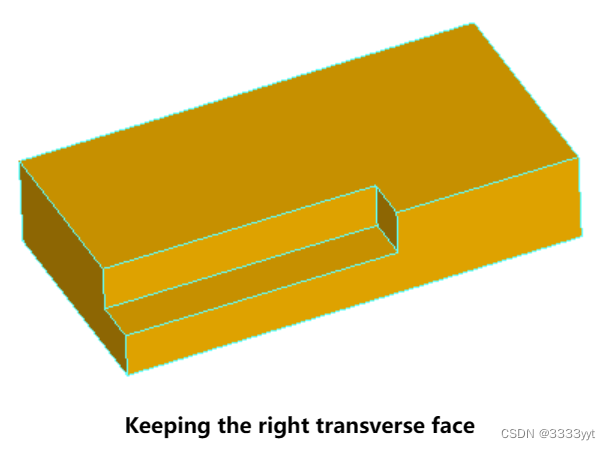
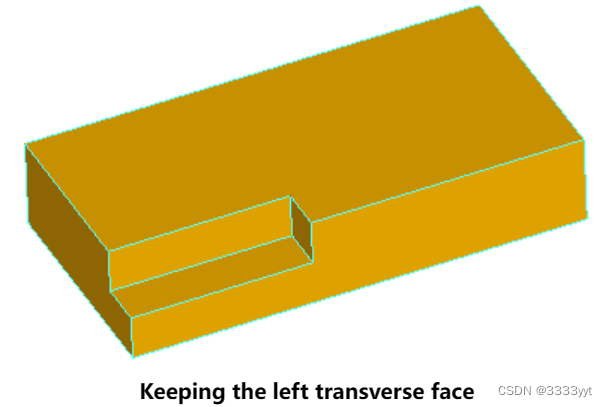
用法
下面是在c++级别使用BrepAlgoApi_Feataturing算法的示例:
TopoDS_Shape aSolid = ...; // Input shape to remove the features from
TopTools_ListOfShape aFeatures = ...; // Features to remove from the shape
Standard_Boolean bRunParallel = ...; // Parallel processing mode
Standard_Boolean isHistoryNeeded = ...; // History supportBRepAlgoAPI_Defeaturing aDF; // Defeaturing algorithm
aDF.SetShape(aSolid); // Set the shape
aDF.AddFacesToRemove(aFaces); // Add faces to remove
aDF.SetRunParallel(bRunParallel); // Define the processing mode (parallel or single)
aDF.SetToFillHistory(isHistoryNeeded); // Define whether to track the shapes modifications
aDF.Build(); // Perform the operation
if (!aDF.IsDone()) // Check for the errors
{// error treatmentStandard_SStream aSStream;aDF.DumpErrors(aSStream);return;
}
if (aDF.HasWarnings()) // Check for the warnings
{// warnings treatmentStandard_SStream aSStream;aDF.DumpWarnings(aSStream);
}
const TopoDS_Shape& aResult = aDF.Shape(); // Result shape
使用API history方法来跟踪形状的历史:
// Obtain modification of the shape
const TopTools_ListOfShape& BRepAlgoAPI_Defeaturing::Modified(const TopoDS_Shape& theS);// Obtain shapes generated from the shape
const TopTools_ListOfShape& BRepAlgoAPI_Defeaturing::Generated(const TopoDS_Shape& theS);// Check if the shape is removed or not
Standard_Boolean BRepAlgoAPI_Defeaturing::IsDeleted(const TopoDS_Shape& theS);
命令removefeatures允许在绘制级别上使用特征化算法。
标准历史命令可用于跟踪特征化过程中形状修改的历史。
有关上述命令的更多详细信息,请参阅绘制测试线束用户指南的Defeatiring commands。
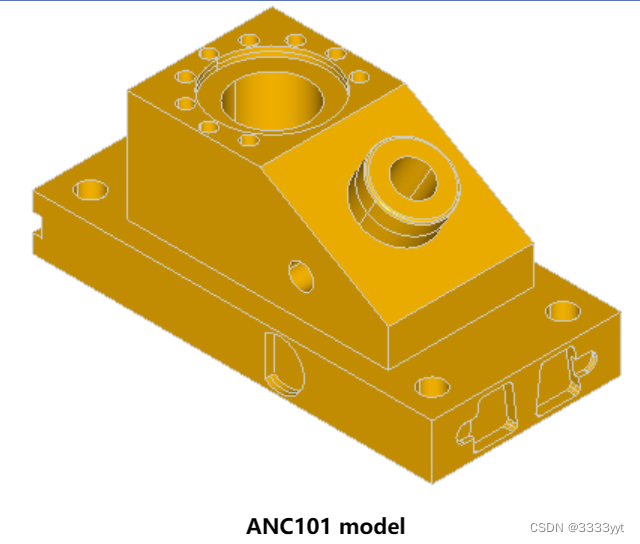
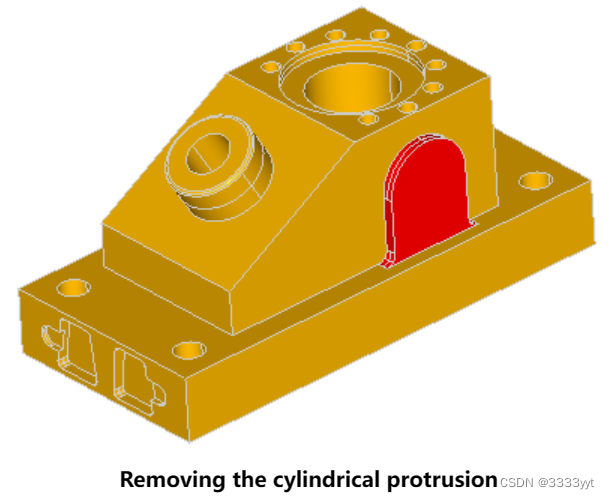
示例
以下是ANC101模型特征的例子:
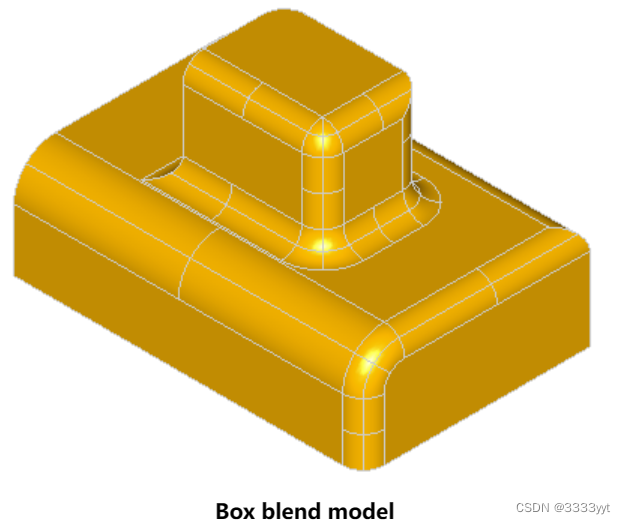
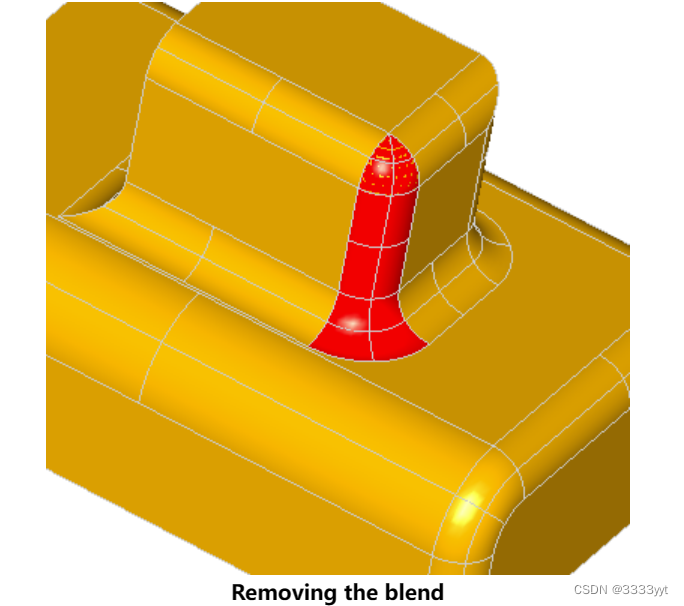
以下是包含混合盒的模型特征的几个例子:
3D 模型周期性
Open CASCADE技术提供了在指定方向的3D空间中制作任意3D模型(或只是形状)周期的工具。
形状的周期性意味着形状可以在任何周期性方向上重复任意次数,而不会产生新的几何形状或分裂。这个算法的思想是使形状在相反的边或者在周期方向的周期边界上看起来相似。这并不意味着该形状的相对侧面将被镜像。它只是意味着形状的对边应该被彼此分开,在对边得到相同的几何形状。这种方法将允许重复形状,即在周期上翻译形状的副本,而不创建新的几何形状,因为不会有不同维度的重合部分。
为了更好地理解周期性的含义,让我们制作一个简单的棱镜,让它具有周期性。下面的绘制脚本创建扩展为10x5x10的l形棱镜:
polyline p 0 0 0 0 0 10 5 0 10 5 0 5 10 0 5 10 0 0 0 0 0
mkplane f p
prism s f 0 5 0
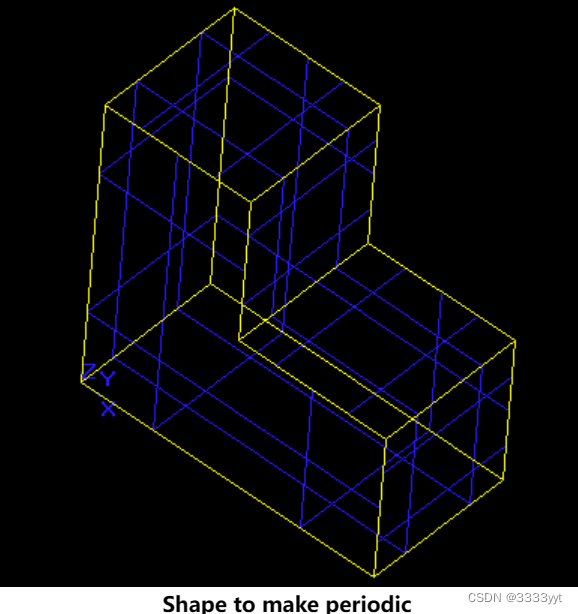
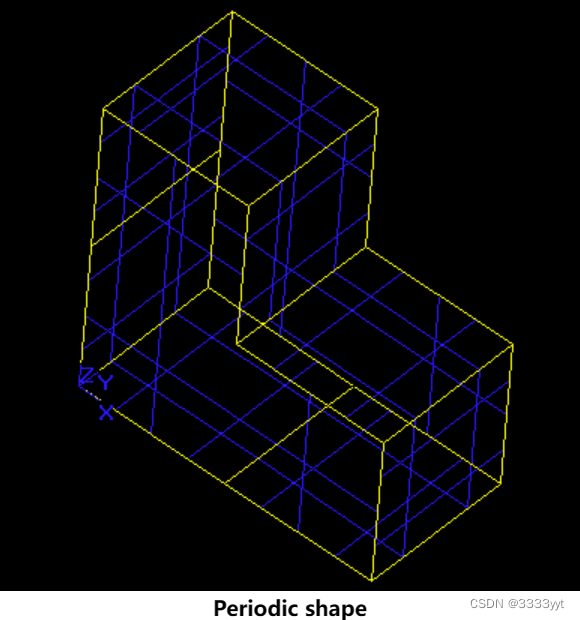
使这个形状在X, Y和Z方向上具有周期性,并且周期与形状的延伸相匹配,应该会使形状的负X和负Z边分裂。形状在Y方向的相对两侧已经相似,因此预计不会有新的分裂。这是把它做成周期性后的形状:
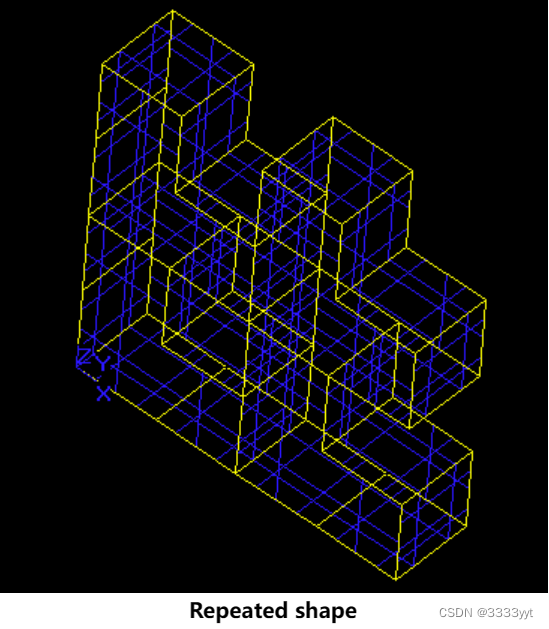
这是形状在X和Z方向上的重复:
OCCT形状周期性工具还允许在周期与形状的扩展不匹配时使形状具有周期性。让这个形状以11 6 11为周期分别对应X, Y, Z周期。这样的周期值意味着在重复的形状之间会有一个间隙,因为在重复的过程中,相反的两边不接触,所以形状根本不会分裂。这是形状在X和Z方向上的重复:
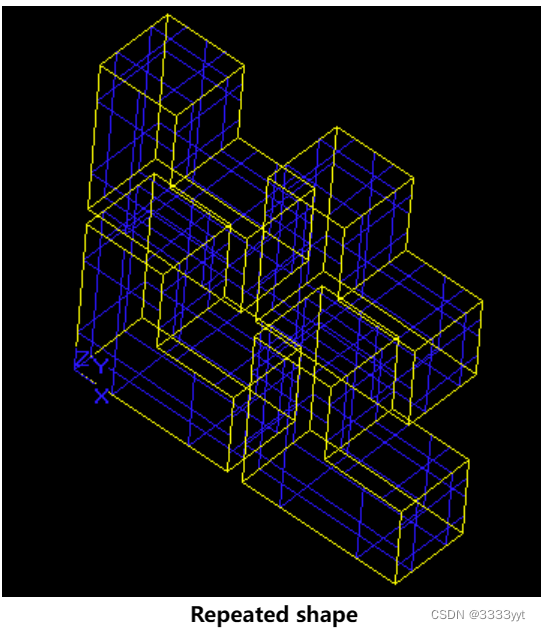
正如预期的那样,形状没有分裂,重复的元素也没有接触。
如果有必要,算法将通过将其与限制形状请求周期的平面分开来修剪形状以适应请求周期。例如,让l形周期仅在X方向上,周期2从X参数4开始:
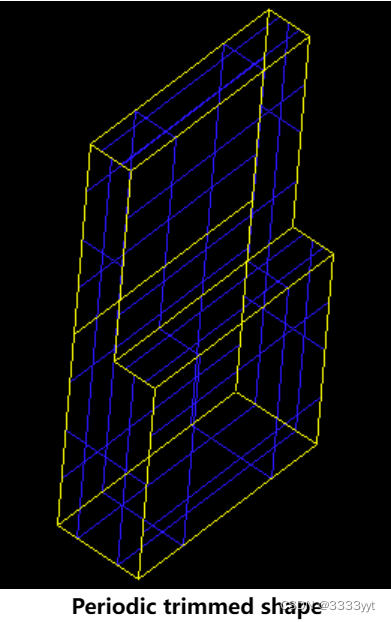
如何使形状具有周期性
为了使形状在一定方向上具有周期性,算法执行以下步骤:
几何形状的重复复制确保周期形状的角边缘在所有周期方向的相对侧具有相同的几何形状。
因此,在周期形状中,形状正侧的几何形状总是复制到周期方向的负侧。
相反形状关联
该算法还将位于周期形状相对两侧的相同(或双胞胎)形状联系起来。通过构造,两个形状应该始终具有相同的几何形状,并且在周期上彼此保持距离。有可能这个形状没有任何双胞胎。这意味着当重复这个形状时,不会碰到形状的另一边。在此示例中,当形状的周期大于其扩展时,子形状中没有一个具有双胞胎。
周期性形状重复
该算法还提供了在周期方向上重复周期形状的方法。为了重复形状,该算法制作所需数量的形状副本,并在time * period值上逐个转换它们。在所有的副本被制作和翻译后,它们被粘在一起,使其具有有效的形状。随后的重复是在重复的形状上进行的,因此,例如,在任何周期方向上重复该形状两次将产生包含三个形状的结果(原始形状加两个副本)。任何方向的单次重复都会产生6个形状。
重复的动作可以清除并重新开始。
历史记录支持
该算法支持形状修改的历史记录,因此可以跟踪形状是如何被周期性地改变的,以及在重复过程中创建了哪些新形状。分裂历史和周期性形状重复历史在这里都是可用的。注意,所有重复的形状都按照生成到历史记录中的方式存储。
BRepTools_History用于历史支持。
错误/警告
该算法支持错误/警告报告系统,该系统允许获得操作过程中发生的错误和警告的扩展概述。一旦出现任何错误,算法就会停止工作。警告允许继续作业,通知用户出错了。该算法返回以下警报:
有关错误/警告报告系统的更多信息,请参阅布尔操作用户指南中的错误和警告报告系统一章。
用法
该算法在类BOPAlgo_MakePeriodic中实现。下面是它在API级别使用的示例:
TopoDS_Shape aShape = ...; // The shape to make periodic
Standard_Boolean bMakeXPeriodic = ...; // Flag for making or not the shape periodic in X direction
Standard_Real aXPeriod = ...; // X period for the shape
Standard_Boolean isXTrimmed = ...; // Flag defining whether it is necessary to trimming// the shape to fit to X period
Standard_Real aXFirst = ...; // Start of the X period// (really necessary only if the trimming is requested)
Standard_Boolean bRunParallel = ...; // Parallel processing mode or singleBOPAlgo_MakePeriodic aPeriodicityMaker; // Periodicity maker
aPeriodicityMaker.SetShape(aShape); // Set the shape
aPeriodicityMaker.MakeXPeriodic(bMakePeriodic, aXPeriod); // Making the shape periodic in X direction
aPeriodicityMaker.SetTrimmed(isXTrimmed, aXFirst); // Trim the shape to fit X period
aPeriodicityMaker.SetRunParallel(bRunParallel); // Set the parallel processing mode
aPeriodicityMaker.Perform(); // Performing the operationif (aPeriodicityMaker.HasErrors()) // Check for the errors
{// errors treatmentStandard_SStream aSStream;aPeriodicityMaker.DumpErrors(aSStream);return;
}
if (aPeriodicityMaker.HasWarnings()) // Check for the warnings
{// warnings treatmentStandard_SStream aSStream;aPeriodicityMaker.DumpWarnings(aSStream);
}
const TopoDS_Shape& aPeriodicShape = aPeriodicityMaker.Shape(); // Result periodic shapeaPeriodicityMaker.XRepeat(2); // Making repetitions
const TopoDS_Shape& aRepeat = aPeriodicityMaker.RepeatedShape(); // Getting the repeated shape
aPeriodicityMaker.ClearRepetitions(); // Clearing the repetitions
请注意,这个类是基于选项类BOPAlgo_Options,它为算法提供了以下选项:
操作过程中获得的所有历史信息存储在BRepTools_History对象中,通过history()方法可用:
// Get the history object
const Handle(BRepTools_History)& BOPAlgo_MakePeriodic::History();
对于在Draw级别使用MakePeriodic算法,已经实现了以下命令:
有关周期性命令的更多详细信息,请参阅绘制测试线束用户指南中的周期性命令。
要在MakePeriodic操作期间跟踪形状修改的历史记录,可以使用标准历史记录命令。
为了能够在运行算法之前访问操作的错误/警告形状,请使用bdrawwarnshapes命令(参见布尔操作的错误和警告报告系统用户指南中的命令用法)。
示例
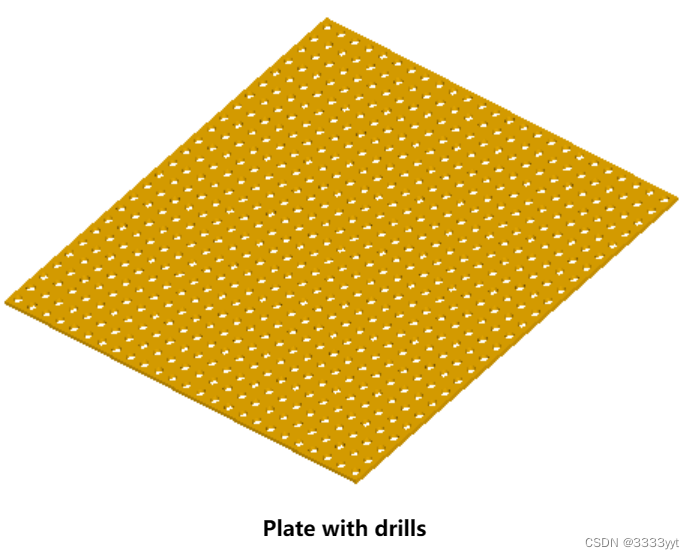
想象一下,你需要在盘子上的钻头彼此之间保持相同的距离。为了模拟这一过程,有必要制作许多圆柱体(模拟钻头)并从板上切割这些圆柱体。使用周期性工具,过程看起来非常简单:
# create plate 100 x 100
box plate -50 -50 0 100 100 1
# create a single drill with radius 1
pcylinder drill 1 1
# locate the drill in the left corner
ttranslate drill -48 -48 0
# make the drill periodic with 4 as X and Y periods, so the distance between drills will be 2
makeperiodic drill drill -x 4 -trim -50 -y 4 -trim -50
# repeat the drill to fill the plate, in result we get net of 25 x 25 drills
repeatshape drills -x 24 -y 24
# cut the drills from the plate
bcut result plate drills
隐线消除
为了提供工业设计所需的精度,图纸需要提供去除隐藏在给定投影中的线条的可能性。
为此,隐线移除组件提供了两种算法:HLRBRep_Algo和HLRBRep_PolyAlgo。
这些算法是基于将要可视化的形状的每个边缘与其每个面进行比较,并计算每个边缘的可见部分和隐藏部分的原理。请注意,这些不是用于生成阴影的算法,阴影算法通过将形状中的每个面部与相同形状的其他面部进行比较来计算形状中每个面部的可见和隐藏部分。这些算法对一个形状进行操作,并去除或显示被面隐藏的边缘。对于给定的投影,他们计算一组被表示对象的特征线。它们还与提取工具一起使用,提取工具从计算结果的选择中重建新的简化形状。这个新形状由边缘组成,代表了投影中可视化的形状。
HLRBRep_Algo允许使用形状本身,而HLRBRep_PolyAlgo使用形状的多面体简化。当你使用HLRBRep_Algo时,你获得了一个精确的结果,然而,当你使用HLRBRep_PolyAlgo时,你减少了计算时间,但获得了多边形段。
没有提供平滑算法。因此,多面体将被视为多面体,算法将以符合多面体数学定义的线段形式给出结果。HLRBRep_PolyAlgo总是这样。
HLRBRep_Algo和HLRBRep_PolyAlgo可以处理任何类型的对象,例如,体,面和线的集合,只要其中没有未完成的对象或点。
然而,在使用HLR时有一些限制:
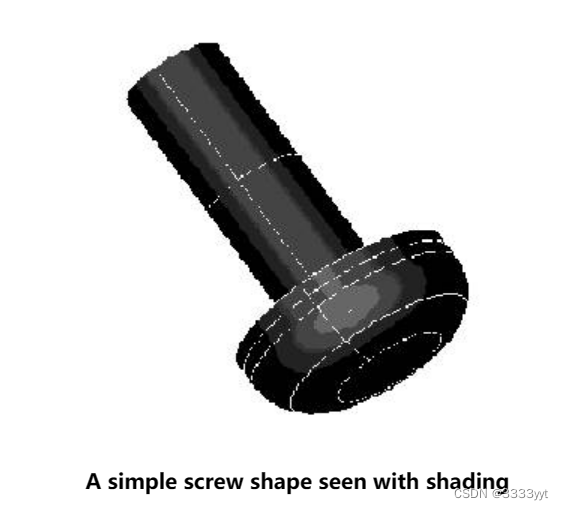
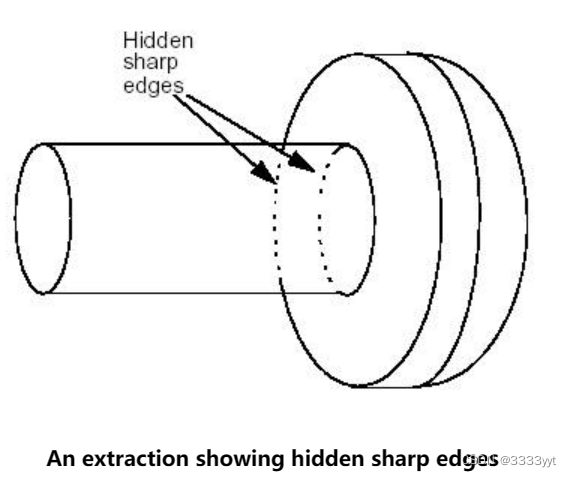
以下服务与删除隐藏线有关:
加载形状
要将TopoDS_Shape传递给HLRBRep_Algo对象,请使用HLRBRep_Algo::Add。对于HLRBRep_PolyAlgo对象,使用HLRBRep_PolyAlgo::Load。如果您希望添加多个形状,请根据需要经常使用add或Load。
设置视图参数
HLRBRep_Algo::Projector和HLRBRep_PolyAlgo::Projector设置了一个投影仪对象,它定义了视图的参数。这个对象是HLRAlgo_Projector。
计算投影
HLRBRep_PolyAlgo::Update启动HLRBRep_PolyAlgo框架可视化的形状轮廓的计算。
对于HLRBRep_Algo,使用HLRBRep_Algo::Update。使用此算法,还必须调用方法HLRBRep_Algo::Hide来计算要可视化的形状的可见和隐藏线。对于HLRBRep_PolyAlgo对象,由HLRBRep_PolyHLRToShape计算可见和隐藏线。
提取边
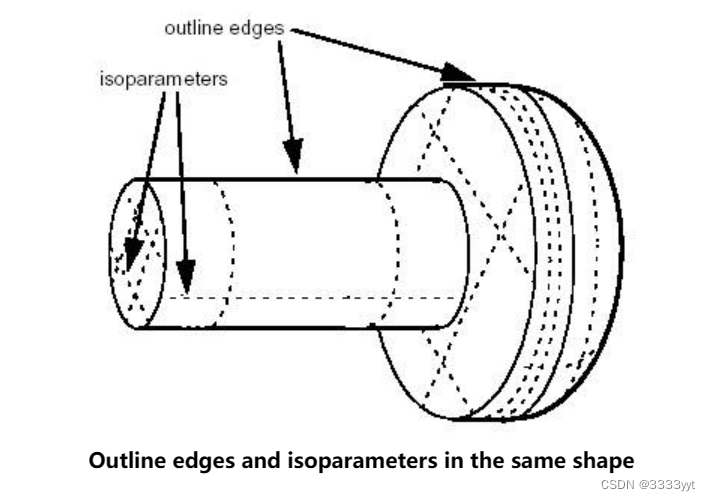
类HLRBRep_HLRToShape和HLRBRep_PolyHLRToShape分别为HLRBRep_Algo对象和HLRBRep_PolyAlgo对象提供了一系列提取过滤器。它们从算法计算的结果中突出显示边缘的类型。使用这两个提取类,你可以突出显示以下类型的输出:
要对HLRBRep_PolyHLRToShape对象执行提取,请使用HLRBRep_PolyHLRToShape::Update函数。
对于由HLRBRepAlgo对象构建的HLRBRep_HLRToShape 对象,您还可以突出显示:
示例
HLRBRep_Algo
// Build The algorithm object
myAlgo = new HLRBRep_Algo(); // Add Shapes into the algorithm
TopTools_ListIteratorOfListOfShape anIterator(myListOfShape);
for (;anIterator.More();anIterator.Next())
myAlgo-Add(anIterator.Value(),myNbIsos); // Set The Projector (myProjector is a
HLRAlgo_Projector)
myAlgo-Projector(myProjector); // Build HLR
myAlgo->Update(); // Set The Edge Status
myAlgo->Hide(); // Build the extraction object :
HLRBRep_HLRToShape aHLRToShape(myAlgo); // extract the results :
TopoDS_Shape VCompound = aHLRToShape.VCompound();
TopoDS_Shape Rg1LineVCompound =
aHLRToShape.Rg1LineVCompound();
TopoDS_Shape RgNLineVCompound =
aHLRToShape.RgNLineVCompound();
TopoDS_Shape OutLineVCompound =
aHLRToShape.OutLineVCompound();
TopoDS_Shape IsoLineVCompound =
aHLRToShape.IsoLineVCompound();
TopoDS_Shape HCompound = aHLRToShape.HCompound();
TopoDS_Shape Rg1LineHCompound =
aHLRToShape.Rg1LineHCompound();
TopoDS_Shape RgNLineHCompound =
aHLRToShape.RgNLineHCompound();
TopoDS_Shape OutLineHCompound =
aHLRToShape.OutLineHCompound();
TopoDS_Shape IsoLineHCompound =
aHLRToShape.IsoLineHCompound();
HLRBRep_PolyAlgo
// Build The algorithm object
myPolyAlgo = new HLRBRep_PolyAlgo(); // Add Shapes into the algorithm
TopTools_ListIteratorOfListOfShape
anIterator(myListOfShape);
for (;anIterator.More();anIterator.Next())
myPolyAlgo-Load(anIterator.Value()); // Set The Projector (myProjector is a
HLRAlgo_Projector)
myPolyAlgo->Projector(myProjector); // Build HLR
myPolyAlgo->Update(); // Build the extraction object :
HLRBRep_PolyHLRToShape aPolyHLRToShape;
aPolyHLRToShape.Update(myPolyAlgo); // extract the results :
TopoDS_Shape VCompound =
aPolyHLRToShape.VCompound();
TopoDS_Shape Rg1LineVCompound =
aPolyHLRToShape.Rg1LineVCompound();
TopoDS_Shape RgNLineVCompound =
aPolyHLRToShape.RgNLineVCompound();
TopoDS_Shape OutLineVCompound =
aPolyHLRToShape.OutLineVCompound();
TopoDS_Shape HCompound =
aPolyHLRToShape.HCompound();
TopoDS_Shape Rg1LineHCompound =
aPolyHLRToShape.Rg1LineHCompound();
TopoDS_Shape RgNLineHCompound =
aPolyHLRToShape.RgNLineHCompound();
TopoDS_Shape OutLineHCompound =
aPolyHLRToShape.OutLineHCompound();
形状连接
Open CASCADE技术提供了使相同维度的触摸形状连接(或粘合)的工具,即使形状之间在拓扑上共享一致的几何形状。为了使形状连接起来,使用通用熔丝算法将它们粘合在一起。使用选项BOPAlgo_GlueShift,因此如果输入形状受到干扰,算法将无法识别这一点。
使一组形状连接起来是有用的,例如,在划分组之前。它将允许生成的网格共形。
使形状连接的算法在类s BOPAlgo_MakeConnected中实现。
材料关联
在这个工具的框架中,输入形状被称为材料,每个输入形状都有一个独特的材料。
连接形状后,输入形状的边界元素与它们所属的形状相关联。这样,就考虑了形状中边界元素的方向。这些关联适用于以下类型:
获取材料信息应采用以下方法
// Returns the original shapes which images contain the given shape with FORWARD orientation.
const TopTools_ListOfShape& BOPAlgo_MakeConnected::MaterialsOnPositiveSide(const TopoDS_Shape& theS)// Returns the original shapes which images contain the given shape with REVERSED orientation.
const TopTools_ListOfShape& BOPAlgo_MakeConnected::MaterialsOnNegativeSide(const TopoDS_Shape& theS)
使连通形状具有周期性
该工具提供了使连接形状周期性的可能性。因为通过使形状周期性,它确保了相反边的重合形状的几何形状将是相同的,它允许为其周期性双胞胎重用形状的网格。
在使形状周期性之后,更新材料关联以对应于结果形状的实际状态。周期形状的重复从这里也是可能的。材料联系不会消失。
历史记录支持
该算法支持操作过程中形状修改的历史记录。除了BRepTools_History提供的标准历史方法(这里用作历史工具)之外,该算法还提供了跟踪反向连接的方法——从生成的形状到输入的形状。这个方法叫做GetOrigins():
// Returns the list of original shapes from which the current shape has been created.
const TopTools_ListOfShape& BOPAlgo_MakeConnected::GetOrigins(const TopoDS_Shape& theS);
这里提供了粘合历史和使形状周期性和周期性形状重复的历史。注意,所有重复的形状都按照生成到历史记录中的方式存储。
错误/警告
该算法支持错误/警告报告系统,该系统允许获得操作过程中发生的错误和警告的扩展概述。一旦出现任何错误,算法就会停止工作。警告允许继续作业,通知用户出错了。该算法返回以下警报:
有关错误/警告报告系统的更多信息,请参阅布尔运算的错误和警告报告系统用户指南一章。
使用语法
以下是BOPAlgo_MakePeriodic算法在API级别上的使用示例:
TopTools_ListOfShape anArguments = ...; // Shapes to make connected
Standard_Boolean bRunParallel = ...; // Parallel processing modeBOPAlgo_MakeConnected aMC; // Tool for making the shapes connected
aMC.SetArguments(anArguments); // Set the shapes
aMC.SetRunParallel(bRunParallel); // Set parallel processing mode
aMC.Perform(); // Perform the operationif (aMC.HasErrors()) // Check for the errors
{// errors treatmentStandard_SStream aSStream;aMC.DumpErrors(aSStream);return;
}
if (aMC.HasWarnings()) // Check for the warnings
{// warnings treatmentStandard_SStream aSStream;aMC.DumpWarnings(aSStream);
}const TopoDS_Shape& aGluedShape = aMC.Shape(); // Connected shape// Checking material associations
TopAbs_ShapeEnum anElemType = ...; // Type of border element
TopExp_Explorer anExp(anArguments.First(), anElemType);
for (; anExp.More(); anExp.Next())
{const TopoDS_Shape& anElement = anExp.Current();const TopTools_ListOfShape& aNegativeM = aMC.MaterialsOnNegativeSide(anElement);const TopTools_ListOfShape& aPositiveM = aMC.MaterialsOnPositiveSide(anElement);
}// Making the connected shape periodic
BOPAlgo_MakePeriodic::PeriodicityParams aParams = ...; // Options for periodicity of the connected shape
aMC.MakePeriodic(aParams);// Shape repetition after making it periodic
// Check if the shape has been made periodic successfully
if (aMC.PeriodicityTool().HasErrors())
{// Periodicity maker error treatment
}// Shape repetition in periodic directions
aMC.RepeatShape(0, 2);const TopoDS_Shape& aShape = aMC.PeriodicShape(); // Periodic and repeated shape
请注意,该类基于选项类BOPAlgo_options,它为算法提供了以下选项:
操作过程中获得的所有历史信息都存储在BRpTools_history对象中,并可通过history()方法获得:
// Get the history object
const Handle(BRepTools_History)& BOPAlgo_MakeConnected::History();
为了在绘图级别上使用MakeConnected算法,已经实现了以下命令:
有关连接命令的更多详细信息,请参阅《绘制测试线束用户指南》中的MakeConnected命令。
要在MakeConnected操作期间跟踪形状修改的历史,可以使用标准历史命令。
要有可能访问操作的错误/警告形状,请在运行算法之前使用bdrawwarnshapes命令(请参阅布尔操作的错误和警告报告系统用户指南中的命令用法)。
标签:
相关文章
-
无相关信息
