纹理特征（一）——GLCM灰度共生矩阵基础

参考文献

[1] HARALICK R M, SHANMUGAM K. Textural features for image classification[J]. IEEE transactions on systems ,man, and cybernetics, 1973 ,3(6):610-621.
[2]王辉,丛榆坤,陈金阳,王敏.基于MATLAB数字图像GLCM纹理分析软件实现[J].数字技术与应用,2019,37(10):146-148+150.
[3]高程程,惠晓威.基于灰度共生矩阵的纹理特征提取[J].计算机系统应用,2010,19(06):195-198.
[4]杨彦荣,宋荣杰,胡国强,张桓.基于随机森林和纹理特征的苹果园遥感提取[J].现代电子技术,2020,43(03):40-44.
（参考文献附上，有需要的可以知网查询原文）

1、灰度共生矩阵简介

1973年Haralick^[1]等人提出了用灰度共生矩阵来描述纹理特征。灰度共生矩阵是分析图像纹理特征的一种重要方法，具有较强的鲁棒性和稳定性，在实际应用中比较广泛。

灰度直方图是对图像上单个像素具有某个灰度进行统计的结果，而灰度共生矩阵是对图像上保持某距离的两像素分别具有某灰度的状况进行统计得到的。

2、数学定义

灰度共生矩阵是从图像灰度值为i的像元（x,y）出发，统计与其距离为d，灰度值为j的像元（x+a,y+b）同时出现的频度P(i,j,d, θ theta θ)。

数学表达式为：
P（i,j,d, θ theta θ）={[(x,y),(x+a,y+b)/f(x,y)=i,f(x+a,y+b)=j]}

其中， θ theta θ为灰度共生矩阵的生成方向，通常去0^°、45^°、90^°、135^°四个方向。
其中，R是正规化常数，是灰度共生矩阵中的全部元素之和。Haralick等人定义了14个用于纹理分析的灰度共生矩阵参数，常用的几个参数即：能量、对比度、熵、相关、逆差矩。

灰度共生矩阵像素对如下：

当两像素间的位置关系d选定后, 就生成一定关系d下的灰度共生矩阵。
共生矩阵的一个元素代表了一种灰度组合下出现的次数。如元素P_d (1, 0) 代表了图像上位置关系为d的两个像素灰度分别为1和0的情况出现的次数。

2.1 角二阶矩（能量）

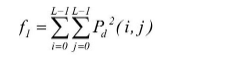
二阶距（Angular Secondmoment）是灰度共生矩阵元素值得平方和，所以也称为能量，反映了图像灰度分布均匀程度和纹理粗细程度。

如果灰度共生矩阵的所有值均相等，则f1小。 如果其中一些值大而其他值小，则f1大。当f1大时，纹理粗，能量大；反之，f1小时，纹理细，能量小。

2.2 对比度

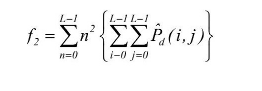
对比度（Contrast）反映了图像的清晰度和纹理沟纹深浅的程度。纹理的沟纹深，其对比度大，效果清晰；反之，对比度小，则沟纹浅，效果模糊。

灰度差即对比度大的像素对越多，这个值越大。灰度共生矩阵中远离对角线的元素值越大，对比度越大。

2.3 相关

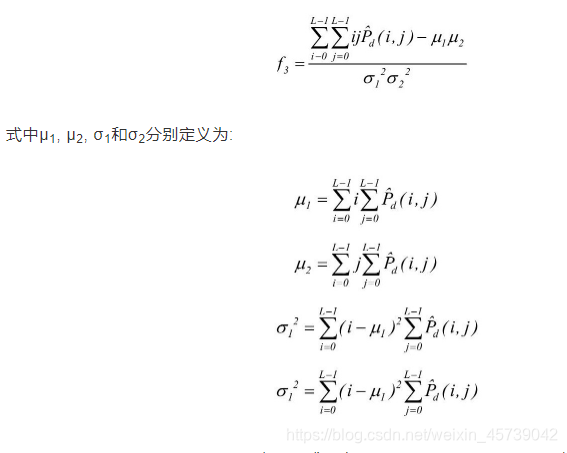
相关（Correlation）是用来衡量灰度共生矩阵的元素在行或列方向上的相似程度。

当矩阵元素值均匀相等时，相关值就大；相反，如果矩阵像素值相差很大则相关值小。如果图像中有水平方向纹理，则水平方向矩阵的相关值大于其余矩阵的相关值。

2.4 熵

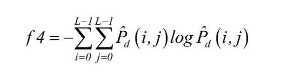
熵（Entropy）是图像具有信息量的度量，纹理信息也属于图像的信息，是一个随机性的度量。它表示图像中纹理的非均匀程度或复杂程度。

若纹理复杂，熵值大；反之，若图像中灰度均匀，共生矩阵中元素大小差异大，熵值小。

若图像没有任何纹理，则灰度共生矩阵几乎为零阵。当灰度共生矩阵中所有元素有最大的随机性、灰度共生矩阵中所有值几乎相等时，共生矩阵中元素分散分布时，熵较大。

2.5 逆差矩

逆差矩（inverse different moment）如果灰度共生矩阵对角元素有较大值，IDM就会取较大的值。因此连续灰度的图像会有较大IDM值。
逆差矩： 反映图像纹理的同质性，度量图像纹理局部变化的多少。其值大则说明图像纹理的不同区域间缺少变化，局部非常均匀。

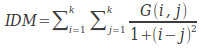
2.6 其他特征

灰度共生矩阵中还有其他的特征，例如：方差、均值和、方差和、差的方差、和熵、差熵、聚类阴影、显著聚类、最大概率。

由于在实际应用中较少，所以在这里不做过多阐述（其实是上述五种特征还没搞明白>.<），刚开始写博客，公式的编辑还没学会，所以复制粘贴的图片，请大家见谅。